TDT4120: Algoritmer og datastrukturer

Tatt høsten 2022. Nedenfor er notater fra alle forelesningene bortsett fra forelesning 14.

01. Problemer og algoritmer

📚Forkunnskaper og pseudokode

Forkunnskaper til emner er logaritmer, spesielt logaritmisk notasjon og regneregler for logaritmer slik at det er enklere å se at teoremer som masterteoremet går opp. Det er i tillegg nødvendig å kjenne til modulo operatoren som er resten av en brøk.

Læreboka er CLRS (https://en.wikipedia.org/wiki/Introduction_to_Algorithms) 4. edition. Boka har gått igjennom betydelige endringer siden 3. edition og anbefales dermed ikke. Pseudokoden i boka antar i de fleste tilfeller at indeksing av lister begynner på 1.

📚Problemløsing og dekomponering

Det finnes mange problemer som datamaskiner kan løse, men ikke alle løsninger til problemene fungerer, spesielt ikke på stor skala.

Eksempel fra forelesning: hvis vi skulle brute-force matching mellom donor og mottaker så hadde vi kun matchet i overkant av hundre personer på 10000000… ganger universets levetid. Dette er estimert til å ta en halvtime for alle menneskene på kloden med Chandran-Hochbaum algoritmen.

Det er derfor viktig at vi bruker en mer optimal løsning for å løse problemet. Hvis vi bruker en ordentlig algoritme istedenfor å brute-force problemet kan vi nå realistiske kjøretider.

Et problem kan beskrives som en general relasjon mellom input og output. Begrepet for en enkel, konkret input er en instans. Siden algoritmer ofte jobber på en eller annen type datastruktur som en liste eller et tre kan det være nyttig å dekomponere problemet i mindre problemer (instanser).

På denne måten kan vi følge en metode lik matematisk induksjon for å skape løsninger for problemene. Vi bryter problemet ned til et “base case” som vi kan bevise at stemmer. Deretter bygger vi opp løsningen ved hjelp av induksjon.

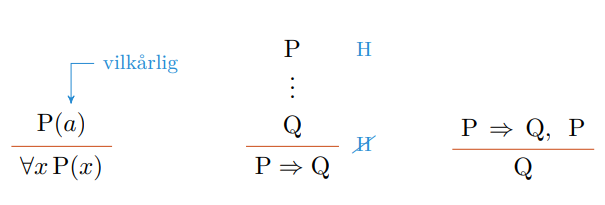
For å gjøre det enklere å bryte opp problemet kan vi bruke følgende tabell for å få en fin mental oversikt over problemet vi ønsker å løse. Først fyller vi ut “Instans” og “Løsning” som tilsvarer input og output til problemet. Deretter jobber vi oss nedover på vestre siden og til slutt går vi opp på høyre side og løser resten av problemet. Nedenfor er eksempel for løsing av insertion-sort.

I kode har vi to måter å løse slike rekursive induksjonsproblemer; løkker og rekursjon. En løkkeinvariant er et delsteg i løsningen for en iterasjon av løsningen til problemet. Vi beviser at løsningen vår er rett for grunntilfellet, og gjennom hvert steg i løkkeinvarianten, beviser at delløsningen er rett både før og etter. På denne måten kan vi induktivt bevise at sluttløsningen vår er riktig. Om dette gjøres ved en faktisk løkke eller rekursjon har ikke noe å si. Som alltid, må vi bevise at løkka eller rekursjonen stopper.

💻Insertion Sort

Insertion Sort er en sorteringsalgoritme som fungerer ved å ta hvert element i lista, og flytte det mot venstre helt til det ligger i riktig posisjon i den sorterte lista. Insertion Sort er en stabil sorteringsalgoritme som betyr at den beholder rekkefølgen på like elementer.

• Best case: $O(n)$ hvis lista er sortert fra før av
• Worst case: $O(n^2)$ hvis lista er sortert fra høyt til lavt (revers)
• Average case: $O(n^2)$

algdat/InsertionSort.scala at main · matsjla/algdat

📚Asymptotisk notasjon

Asymptotisk notasjon er notasjon som ofte brukes for å vise hvor ressurseffektiv en algoritme eller løsning er. Man ser ofte på kjøretid, men man kan også ha asymptotisk notasjon av minnebruk, instruksjonssykluser og liknende data. Nedenfor er skalaen på de forskjellige formene.

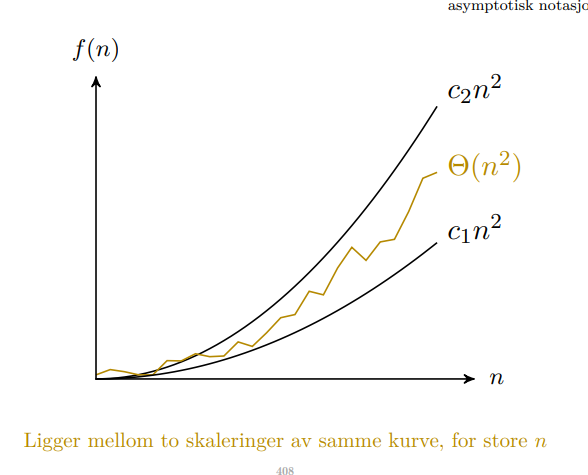
Når vi bruker asymptotisk notasjon er vi kun interessert i en veldig grov størrelsesorden. Dermed dropper vi konstanter og lavere ordens ledd.

$$\Theta(n^2 + n + 10) = \Theta(n^2)$$

Reell eller nøyaktiv kjøretid kan være varierende eller udefinert. Vi ønsker dermed å finne en form som likner kurven. Vi bruker tre forskjellige målinger i asymptotisk notasjon. Det er viktig å vite at det finnes ingen direkte sammenheng mellom $O(n)$, $\Theta(n)$, og $\Omega(n)$ og best/worst/average case kompleksitet for en algoritme. Asymptotisk notasjon er bare en måte å definere best/worst/average case.

• $O(n)$ eller big-o definerer den øvre grensa. Dette betyr at funksjonen kan være opptil $n$ i kompleksitet, men også veldig mye mindre.
• $\Theta(n)$ eller stor theta definerer “tightest bound”. Dette betyr at funksjonen vil være tilnærmet $n$. Det impliserer også $O(n) = \Omega(n) \implies \Theta(n)$
• $\Omega(n)$ eller stor omega definerer den nedre grensa. Dette betyr at funksjonen har ihvertfall $n$ i kompleksitet, men det er ingen øvre grense som betyr at den kan være uendelig kompleks.

I tillegg har vi $o(n)$ og $\omega(n)$ som er øvre, men ikke lik, og nedre, men ikke lik grenser.

Når en skal regne på asymptotisk notasjon hjelper det å tenke på at notasjonen $O(n)$ definerer mengden av alle funksjonene med kompleksitet $n$ eller mindre. Det resulterer ofte iat $\Omega(n)$ dominerer et uttrykk. Dessuten er $f(n) = O(n)$ notasjon misbruk da $O(n)$ er en mengde.

---

02. Datastrukturer

💻Stack

En Stack er en lineær last-in-first-out (LIFO) datastruktur. En stack fungerer som en stabel hvor elementene som legges på først, kommer ut sist. Relevant funksjonalitet på en Stack i pensum er:

• $StackEmpty$ - er stacken tom?
• $StackPush$ - legg til et element på toppen av stacken i konstant tid $O(1)$
• $StackPop$ - fjern et element fra toppen av stacken i konstant tid $O(1)$

algdat/Stack.scala at main · matsjla/algdat

💻Queue

En Queue er en lineær first-in-first-out (FIFO) datastrukturo. En Queue fungerer på lik måte som en Stack, bortsett fra at elementene som ble lagt på først, kommer ut først. Relevant funksjonalitet på en Queue fra pensum er:

• $QueueEnqueue$ - legg til et element i køen i konstant tid $O(1)$
• $QueueDequeue$ - ta det fremste elementet i køen i konstant tid $O(1)$
• $QueueSize$ - størrelsen på køen, som regel kun relevant hvis køen ikke backes av en resizable container.

Implementasjonen i pseudokode i pensum tar ikke hensyn til overflow eller underflow av køen. Implementasjon i Scala tar hensyn til dette.

algdat/Queue.scala at main · matsjla/algdat

💻LinkedList

En lenket liste (i pensum, doubly-linked-list) er en liste som består av noder som er allokert tilfeldige steder i minnet som er koblet sammen via pekere. Det tar dermined lineær tid å slå opp på en gitt posisjon, men det er konstant tid for å sette inn eller slette elementer. Relevant funksjonalitet på en LinkedList fra pensum er:

• $ListSearch$ - søk igjennom en liste. Beste tilfelle på $O(1)$ hvis første element er søkeelementet, ellers er det gjennomsnittslig og verste tilfelle på $O(n)$.
• $ListPrepend$ - legg til en node i frontend av lista i konstant tid $O(1)$.
• $ListInsert$ - legg til en ny node $x$ foran en eksisterende node $y$ i konstant tid $O(1)$. Denne funksjonen trenger ikke et liste objekt da den kun operer på to noder.
• $ListDelete$ - slett en node $x$ fra lista i konstant tid $O(1)$

algdat/LinkedList.scala at main · matsjla/algdat

💻HashTable

En hashtabell er en relasjon eller mapping mellom en nøkkel på en verdi. En hashtabell implementeres som regel ved hjelp av en lineær datastruktur av LinkedList-er. Nøkkelen går igjennom en hash-funksjon som bestemmer hvilken bøtte verdien skal havne i. En god hash-funksjon vil ha så få kollisjoner som mulig som gjør innsetting til, og henting fra tabellen ta konstant tid.

I tilfelle hvor det er kollisjoner, lagres også noe ekstra data (gjerne nøkkelen eller annen data som kan gjenkjenne nøkkelen) for å løse kollisjoner. Dette resulterer i veldig simple algoritmer for å bruke hashtabellen. Relevant funksjonalitet på et HashTable fra pensum er:

• $ChainedHashSearch$ - finn verdien til en nøkkel i hashtabellen. Kjører i beste og gjennomsnittslig tilfelle i konstant tid $O(1)$, men siden det kan være kollisjoner er verste tilfelle $O(n)$.
• $ChainedHashInsert$ - sett inn gitt nøkkel og verdi i lista i konstant tid $O(1)$.
• $ChainedHashDelete$ - fjern verdien til en nøkkel i hashtabellen. Kjører i beste og gjennomsnittslig tilfelle i konstant tid $O(1)$, men siden det kan være kollisjoner er verste tilfelle $O(n)$.

algdat/HashTable.scala at main · matsjla/algdat

💻DynamicTable

En dynamisk tabell er en liste eller et array som har evnen til å gro eller minke i størrelse basert på antall elementer i lista. Det betyr at lista kan bli (i teorien) uendelig stor siden vi kan gro lista når den nærmer seg full. Det er vanlig å bruke en større faktor enn $n+1$ for å gro tabellen for å unngå mange allokasjoner. Relevant funskjonalitet på et DynamicTable fra pensum er:

• $TableInsert$ - legg til et nytt element i den dynamiske lista. Kjører beste og gjennomsnittslig tilfelle i konstant tid $O(1)$, men siden lista må gro innimellom er verste tilfelle $O(n)$.

algdat/DynamicTable.scala at main · matsjla/algdat

📚Amortisert arbeid

Kjøretiden for én enkelt operasjon er ikke alltid like informativt. I en dynamisk tabell kan en insert operasjon få lista til å gro og dermed bli $O(n)$, men siden vi får en større grofaktor vil dette som regel ikke skje. Amortisert arbeid er aggregert analyse av et problem. Vi finner totalt arbeid og deler på antall operasjoner.

Average-case kommer dermed av forventet kjøretid for en algoritme, selv om den kan i noen tilfeller være mye tregere (som i $DynamicTableInsert$). Amortisert arbeid er snitt over operasjoner.

---

03. Splitt og hersk

📚Splitt og hersk

Splitt og hersk er et paradigme for å bryte ned et kompleks problem inn i mindre underproblemer og løse underproblemene for seg selv. Deretter setter vi sammen delløsningene for å lage en induktivt riktig løsning.

📚Rekurrenser

Rekurrenser er rekursive likninger, gjerne på formen $f(n) = f(n - 1) + c$. Problemet med slike definisjoner er at de er rekursive som betyr at vi kan prøve å løse de, men utfordringen er å komme seg til bunns og deretter nøste seg opp igjen.

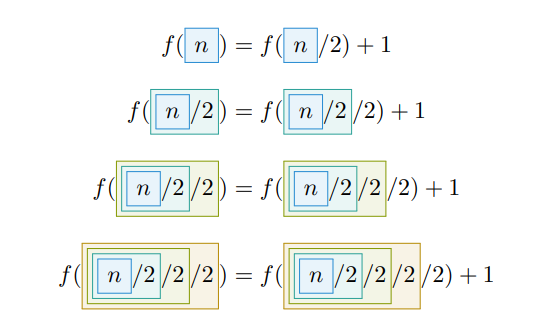
Rekurrenser har som regel et grunntilfelle som gjør det enklere å nå bunnen.

$$f(n) = \begin{cases}n = 1 & 1\\n \neq 1 & f(n - 1) + 1\end{cases}$$

Rekurrenser er nyttige fordi de kan beskrive kompleksiteten eller kjøretiden til rekursive algoritmer. Vi kan løse rekurrenser med:

• Iterasjonsmetoden: gjenntatt ekspandering av rekurrensen til vi får en sum vi kan regne ut
• Rekursjonstrær: ekspander rekurrensen og lag et tre man kan summere på. TODO
• Masterteoremet: en enkel måte å løse rekurrenser av formen $T(n) = a \cdot T(\frac{n}{b}) + f(n)$. Mer om masterteoremet kommer senere i notatet.

Til slutt verifiserer vi løsningen vår med induksjonsbevis.

💻Binary Search

Binærsøk er en divide & conquer søkealgoritme som opererer på en sortert liste. Den velger elementet i midten av lista og sammenligner det med søkeelementet, og kaller seg selv rekursivt på enten høyre eller venstreside av lista. Grunntilfellet er en tom liste hvor vi kan konkludere med at elementet ikke eksisterer i lista.

• Best case: $O(1)$ hvis søkeelementet er i midten av lista
• Worst case: $O(\lg n)$ siden rekursjonstreet har høyde $\lg n$
• Average case: $O(\lg n)$

algdat/BinarySearch.scala at main · matsjla/algdat

💻Merge Sort

Merge Sort er en divide & conquer sorteringsalgoritme. Den drives av subprosedyren $Merge$ som tar inn en liste, splitter det i to og sorterer sublistene. Siden merge kalles etter de rekursive kallene til $MergeSort$ vil det via induksjon bevises at halvsidene av lista er sortert før de merges. Grunntilfellet er en tom liste hvor det ikke finnes mer arbeid å gjøre.

• Best case: $O(n \lg n)$
• Worst case: $O(n \lg n)$
• Average case: $O(n \lg n)$

Kompleksiteten blir $O(n \lg n)$ fordi $Merge$ har en kompleksistet på $n$, ganget med høyden på rekursjonstreet som er $\lg n$.

algdat/MergeSort.scala at main · matsjla/algdat

💻Quick Sort

Quick Sort er en divide & conquer sorteringsalgoritme. Den drives av subprosedyren $Partition$ som velger et pivotelement som plasseres på riktig plass i den sorterte lista, samtidig som den sørger for at alle elementer til venstre er lavere, og alle til høyre er høyere. Siden partition kalles før det rekursive kallet til $QuickSort$ partisjoneres alle breakpoints i lista og dermed kan vi ved induksjon bevise at lista er sortert. Grunntilfellet er tom liste hvor det ikke finnes mer arbeid å gjøre.

• Best case: $O(n \lg n)$
• Worst case: $O(n^2)$ hvis lista var sortert fra før av og pivot velges som siste element
• Average case: $O(n \lg n)$

For å unngå tilfellet hvor dårlig valg av pivot oppstår finnes en alternativ måte å velge pivot på; randomisert Quick Sort. Her vil verste tilfelle bli $O(n \lg n)$ når $n \to \infty$ ettersom det blir tilnærmet null sjanse for at verste tilfellet oppstår.

algdat/QuickSort.scala at main · matsjla/algdat

algdat/RandomizedQuickSort.scala at main · matsjla/algdat

📚Masterteoremet

Masterteoremet er en veldig enkel metode for å løse rekurrenser på formen $T(n) = a \cdot T(\frac{n}{b}) + f(n)$. Her gjelder det bare å vite at $a^{\lg n} = n^{\lg a}$. Ved å se på hvordan logaritmen skisses på grafen er det enkelt å se at disse to er like.

Vi kan bruke iterasjonsmetoden for å finne et mønster i den rekursive funksjonen. Vi får dermed en løsning på formen $a^?T(\frac{n}{b^?})$. Her setter vi inn $? = \lg_b n$.

$$a^{\lg_b n} \cdot T(\frac{n}{b^{\lg_b n}}) \\ a^{\lg_b n} \cdot T(\frac{n}{n}) \\ a^{\lg_b n} \cdot 1 \\ a^{\lg_b n} \\ n^{\lg_b a}$$

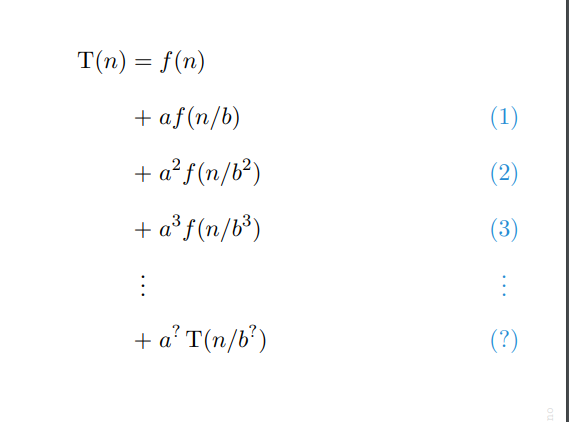
Til slutt sammenligner vi resultatet med den drivende funksjonen $f(n)$.

---

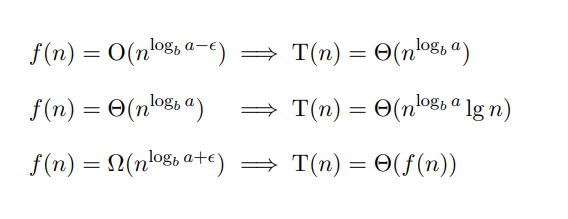
04. Rangering i lineær tid

📚Sortingsgrensen

Det finnes en nedre grense for hvor raske rangeringsalgoritmer kan være. Denne grensa er på $\Omega(n \lg n)$. Dette er synlig i divide-and-conquer algoritmer som deler opp problemet på en måte som gjør det mulig å forestille seg et rekursjonstre.

https://cs.stackexchange.com/questions/32311/proving-the-lower-bound-of-compares-in-comparison-based-sorting/32312#32312

Likevel finnes det algoritmer som $InsertionSort$ som kjører i $O(n)$ i beste tilfelle, men det er kun på grunn av hvordan algoritmen er skrevet. Dessuten kan vi utnytte sorteringsgrensen, og til og med bryte den ved å skrive smarte algoritmer. Et eksempel på dette er $RandomizedSelect$ som kommer senere. Her er generell tabell for sorteringsgrensa.

	Best	Average	Worst
$O$	$O(\infty)$	$O(\infty)$	$O(\infty)$
$\Theta$	$\Theta(?)$	$\Theta(?)$	$\Theta(?)$
$\Omega$	$\Omega(n)$	$\Omega(n \lg n)$	$\Omega(n \lg n)$

Det er umulig å si noe om den generelle øvre grensa ettersom algoritmen kan ta uendelig med tid for alt vi vet. Dessuten er det ikke mulig å gå lavere enn $n$ fordi vi må garantere at hele sekvensen behandles.

📚Reduksjonsbevis

Vi kan bevise egenskaper til enkelte problemer ved å bruke de som del-løsning av et annet problem. Dette kalles reduksjonsbevis. Et eksempel på dette er unikhetsproblemet.

I dette problemet blir vi fortalt at man kan i verste tilfelle finne ut om en tabell har duplikater i $\Omega(n \lg n)$ tid. Siden sortering er mesteparten av arbeidet løsningen kan det umulig ha seg at sortering i verste tilfelle er bedre enn $\Omega(n \lg n)$.

I forelesning 4 presenteres en analogi for reduksjonsbeviset med en låst kiste. Det kan umulig være lettere å åpne kista enn det er å åpne låsen.

💻Randomized Select

Randomized Select er en divide & conquer algoritme som effektivt fungerer som “QuickSort som BinarySearch”. Randomized Select finner elementet på $i$-ende indeks i lista. Vi bruker faktum at $Partition$ subprosedyren til $QuickSort$ plasserer pivotelementet på riktig plass, og sørger for at elementene til vestre er lavere, og elementene til høyre er høyere. På denne måten kan vi splitte lista igjen og finne elementet på en gitt indeks.

• Best case: $O(n)$ av rekurrensen $2n - 1$
• Average case: $O(n)$
• Worst case: $O(n^2)$ hvis pivotelementet er alene, slik som i $QuickSort$. Lite sannsynlig til å skje med randomisering.

I tillegg finnes en annen select algoritme som heter $Select$. Denne er mer kompleks og grundig forståelse er ikke et krav i pensum.

algdat/RandomizedSelect.scala at main · matsjla/algdat

💻Counting Sort

Counting Sort er en stabil sorteringsalgoritme som bryter sorteringsgrensen ved å gjøre en antakelse at ingen elementer er høyere enn en gitt verdi $k$. Deretter lager den en liste som holder styr på hvilken indeks ethvert element i lista skal være i den endelige lista.

• Best case: $\Theta(n + k)$
• Worst case: $\Theta(n + k)$
• Average case: $\Theta(n + k)$

algdat/CountingSort.scala at main · matsjla/algdat

💻Radix Sort

Radix Sort er en stabil sorteringsalgoritme som bryter sorteringsgrensen ved å gjøre en antaklese at ingen elementer har flere enn $d$ siffer. Deretter bruker den en stabil sorteringsalgoritme som $CountingSort$ til å sortere etter hvert siffer.

• Best case: $\Theta(d(n + k)$
• Worst case: $\Theta(d(n + k)$
• Average case: $\Theta(d(n + k)$

algdat/RadixSort.scala at main · matsjla/algdat

💻Bucket Sort

Bucket Sort er en sorteringsalgoritme som bryter sorteringsgrensen ved å anta at alle verdier er flyttall mellom $[0, 1)$ på en uniform distribusjon. Den deler elementene opp i $n$ bøtter, og siden distribusjonen skal være uniform kommer det ikke til å være mange tall i hver bøtte. Dermed slår den sammen alle listene. Bucket Sort er stabil hvis sorteringsalgoritmen den bruker er stabil.

• Best case: $O(n)$
• Worst case: $O(n^2)$
• Average case: $O(n)$

algdat/BucketSort.scala at main · matsjla/algdat

05. Rotfaste trestrukturer

📚Trær

Trær er en betegnelse for grafer uten sykluser hvor antall kanter er antall noder minus 1, $|E| = |V| - 1$. Et binærtre er et tre hvor hver node har 0-2 barn. Et komplett binærtre er et binærtre hvor alle løvnodene ligger på samme høyde med null barn. Et komplett binærtre har alltid $2^x$ løvnoder når høyden er $x$. Derav ser vi også at høyden av et tre med $n$ noder blir $\lg n$.

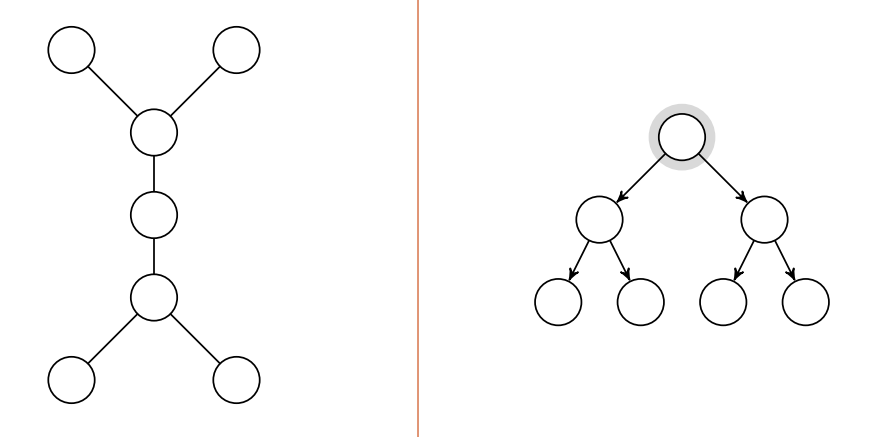
Det finnes flere klasser trær:

• Et ordnet tre definerer en ordning på barna
• Et posisjonstre har hvert barn en posisjon, og barn kan mangle.
• Et binærtre er et posisjonstre hvor hvert barn har to barneposisjoner.

CLRS definerer ikke binærtrær som trær, men vi kan godt tolke dem som ordnede trær med ekstra informasjon. Dessuten kan det være hensiktsmessing å se på binærtrær som grafer. I noen tilfeller kan kantene i binærtreet ha piler. Det er dermed også en directed-acyclic-graph (DAG).

Når vi skal traversere treet har vi et par muligheter. I hvilken rekkefølge skal vi håndtere den nåværende noden før vi fortsetter ned treet? Vi har tre muligheter:

• Inorder: besøk alle nodene til venstre, deretter seg selv, og til slutt de på høyre. Dette blir riktig rekkefølge for binære søketrær.
• Preorder: besøk seg selv, deretter noder til venstre og høyre
• Postorder: besøk noder til venstre og høyre, deretter seg selv

Det er kun $InorderTreeWalk$ som er implementert i pensum. Det er dermed åpenbart at kompleksiteten til traversering av et tre med $n$ noder er $\Theta(n)$.

algdat/InorderWalk.scala at main · matsjla/algdat

📚Binære søktrær

Binære søketrær er funksjonelt sett binærsøk i form av en datastruktur. Barnet til venstre har lavere verdi, og det til høyre har en høyere verdi. På denne måten blir det veldig lett å navigere treet.

Det er også greit å merke seg at binære søketrær i pensum ikke håndterer duplikater.

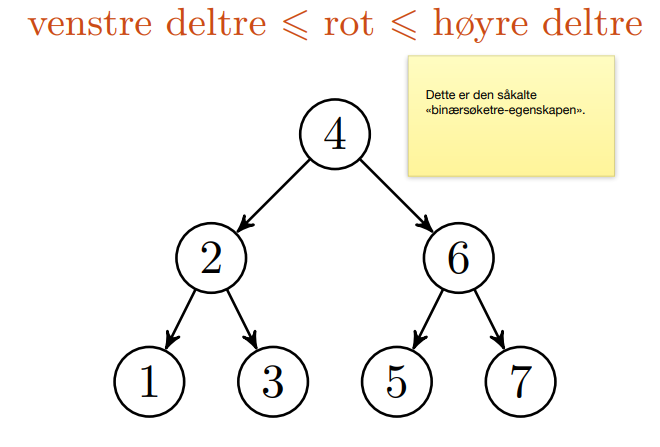
Relevant funksjonalitet på et BinarySearchTree fra pensum er:

• $TreeSearch$ - søk for en verdi i treet på kjøretid $O(\lg n)$, eller $O(1)$ hvis rot er tom eller søkeverdi.
• $TreeInsert$ - sett inn et nytt tall i treet i $O(\lg n)$ tid, eller $O(1)$ hvis treet er tomt.
• $TreeMinimum$ - finn minimumverdien treet i $O(\lg n)$ tid, eller $O(1)$ hvis treet er tomt.
• $TreeMaximum$ - finn maksverdien i treet i $O(\lg n)$ tid, eller $O(1)$ hvis treet er tomt.
• $TreeSuccessor$ - finn noden med minste verdi som er større en den gitte noden i $O(\lg n)$ tid.
• $TreeDelete$ - slett et element fra treet i $O(\lg n)$ tid.

algdat/BinarySearchTree.scala at main · matsjla/algdat

📚Hauger

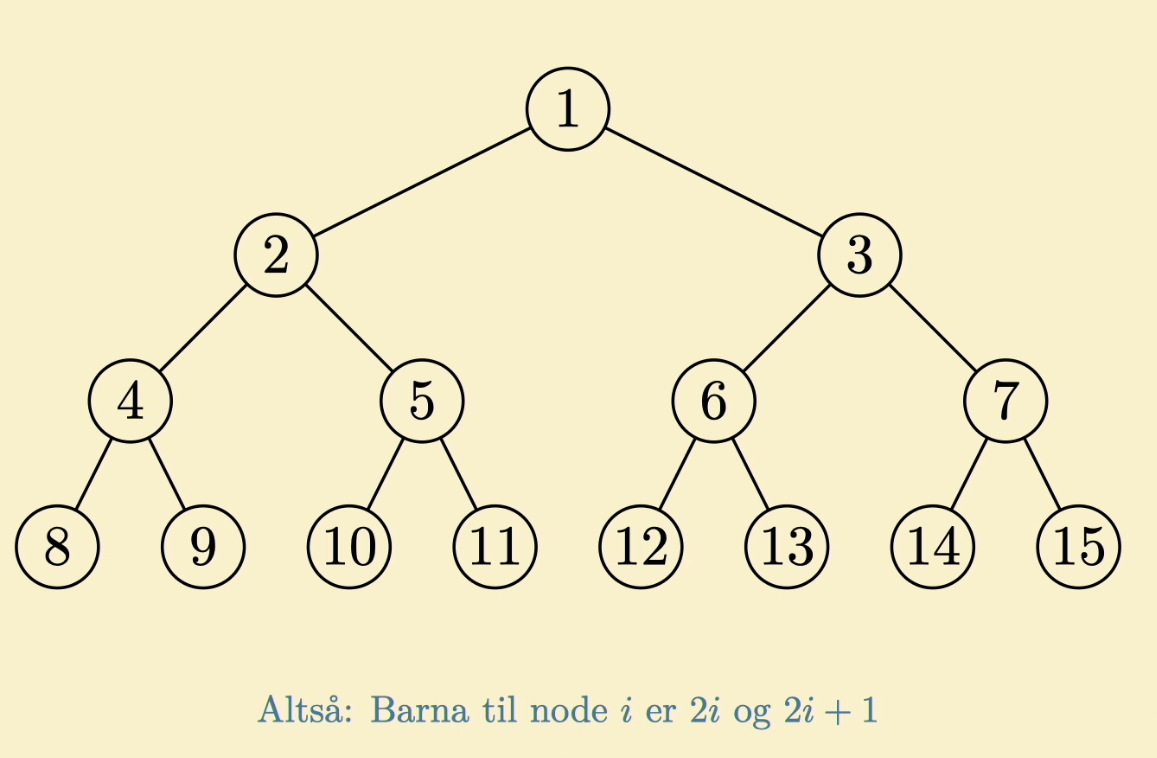
En haug er en datastruktur. I bunn og grunn er en haug en liste eller et array, men vi forestiller oss at haugen er et tre.

Med denne tolkningen kan vi få tilgang til barna eller foreldrene til en node. Hauger er automatisk så balanserte som mulig.

Vi ser ofte på $MaxHeap$ eller $MinHeap$ versjoner av hauger. Dette gir oss en gylden mulighet til å implementere prioritetskøer.

Hauger trenger ikke å være sorterte, og siden det finnes eksponensielt mange lovlige rekkefølger, gjelder ikke sorteringsgrensen.

Relevant funksjonalitet på en Heap fra pensum er:

• $HeapLeft$: finn posisjonen barnet til venstre til en node i konstant tid $O(1)$.
• $HeapRight$: finn posisjonen barnet til høyre til en node i konstant tid $O(1)$.
• $HeapParent$: finn posisjonen foreldrenoden til en node i konstant tid $O(1)$.
• $MaxHeapify$: omplasserer en gitt node og barna til noden slik at den følger max-heap egenskapen i $O(\lg n)$ tid, men konstant $O(1)$ i beste tilfelle.
• $BuildMaxHeap$: bygg et MaxHeap av et array i lineær tid $O(n)$.

I tilfellet hvor haugen brukes som en prioritetskø ønsker vi oss følgende funksjonalitet (som også er pensum):

• $HeapMax$: finn den største verdien i haugen i konstant tid $O(1)$.
• $HeapExtractMax$: finn og fjern det største elementet i haugen i logaritmisk tid $O(\lg n)$.
• $HeapIncreaseKey$: øk verdien til en nøkkel i haugen i logaritmisk tid $O(\lg n)$.
• $MaxHeapInsert$: sett inn en ny verdi inn i haugen i logaritmisk tid $O(\lg n)$.

💻HeapSort

Til slutt kan vi bruke disse funksjonene til å implementere en sorteringsalgoritme ved hjelp av en haug. Denne algoritmen heter $HeapSort$.

• Best case: $O(n)$
• Worst case: $O(n \lg n)$
• Average case: $O(n \lg n)$

---

06. Dynamisk programmering

📚Optimal delstruktur

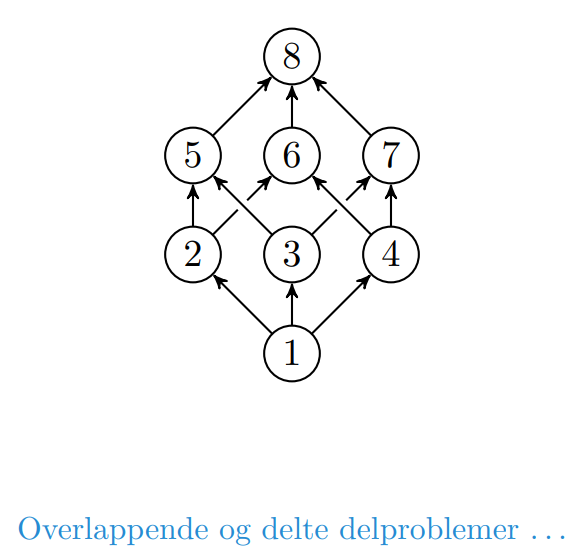
Optimal delstruktur er en egenskap et problem kan ha, og er nødvendig for at problemet kan ha en løsning med dynamisk programmering. I tillegg må problemet ha overlappende delinstanser. Når et problem har overlappende delinstanser betyr det at flere oppdelinger av problemet inneholder noen av de samme delinstansene.

At et problem har optimal delstruktur betyr at det løsningen til problemet kan konstrueres fra optimal løsninger på delinstanser av problemet.

Det vil dermed være optimalt å cache eller lagre svaret på delinstansene slik at man slipper å regne ut løsningen når problemet oppstår igjen.

Man kan generelt se på dynamisk programmering som et “Time-memory tradeoff” hvor vi ofrer minne for å lagre delløsninger, men i gjengjeld kan vi spare mye tid.

💻Rod Cutting Problem

Stavkapproblemet er et eksempel på et problem som kan løses optimal ved hjelp av dynamisk programmering.

En dum løsning på dette problemet kan oppnås ved å prøve alle kombinasjonene rekursivt, og til slutt oppnå en kjøretid på $O(2^n)$. Dette er ikke bra nok!

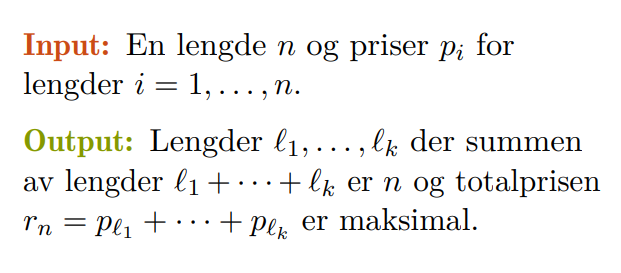
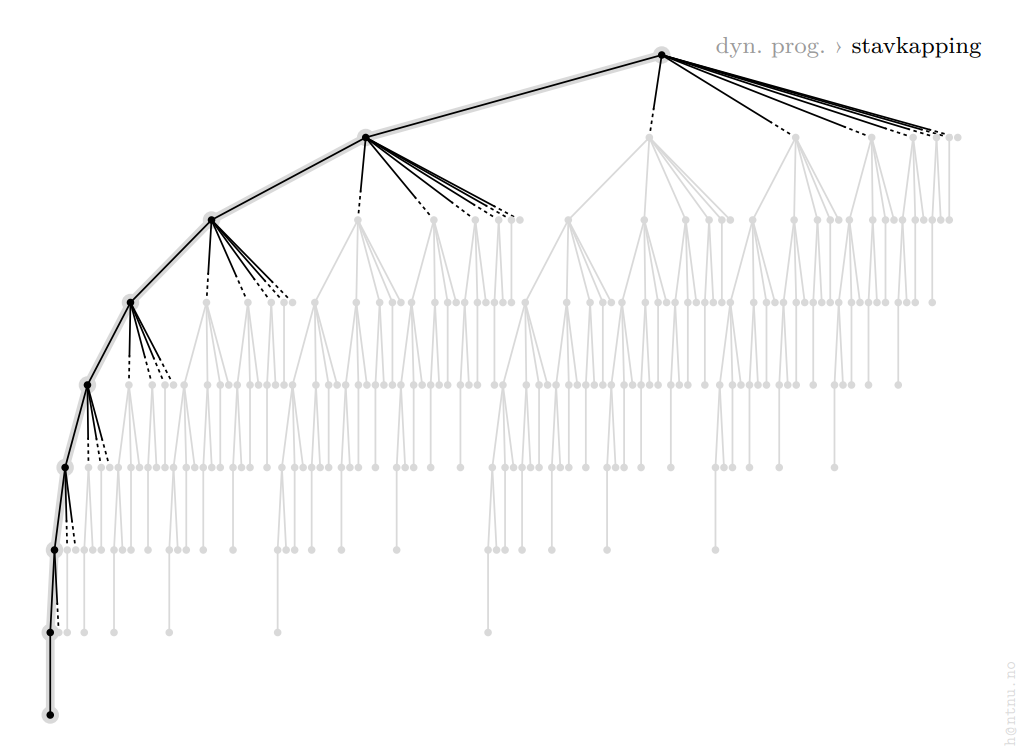
En optimal løsning vil lagre løsningene på de forrige verdiene, og det blir dermed mulig å slå opp løsningen på tidligere delproblemer. Grafen nedenfor illustrerer hvor mange kalkulasjoner som spares på denne måten.

📚Bottom-up iterasjon vs top-down memoisering

Det finnes to hovedmetoder for å programmere en løsning som utnytter dynamisk programmering; bottom-up og top-down. Forskjellen på metodene handler om hvordan man designer løsningen til å utføre kallene på delproblemene.

• Top-down: du begynner på hovedproblemet og finner ut hvilke delløsninger som er mulige for å komme seg dit. Her er det vanlig å bruke rekursjon og memoisering av funksjoner.
• Botton-up: du finner ut av hvilke delløsninger som kommer til å måtte løses, og løser disse. Deretter jobber du deg opp mot hovedproblemet og bruker de tidligere løsningene. Denne metoden kalles ofte tabulation fordi du fyller gjerne inn delløsningene i en tabell.

💻Matrisekjedemultiplikasjon

Matrisekjedemultiplikasjon er en et problem hvor vi ønsker å finne den optimale måten å gange sammen en kjede (liste) med matriser av ulik størrelse $\langle A_1, A_2, … , A_n \rangle$. =

Hvis vi har fire matriser, finnes det fem unike måter å gange disse sammen på, og basert på størrelsen på hver av matrisene kan antallet kalkulasjoner variere stort.

Hvis vi prøver å gange sammen matrisene slik som vi vanligvis hadde gjort, kan det hende vi gjør unødvendig mange kalkulasjoner.

Fire matriser har 5 unike måter å ganges sammen

💻Longest common subsequence

Gitt to sekvenser ønsker vi å finne den lengste subsekvensen som er lik i begge sekvensene.

Hvis vi prøver å løse problemet ved hjelp av brute-force finner vi fort ut at vi får et eksponensielt stort problem som vil være ubrukelig ved store $n$.

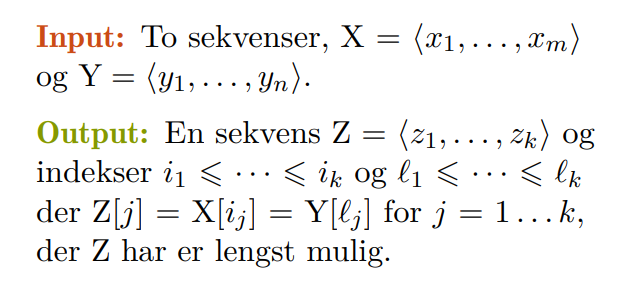
💻Binære ryggsekkproblemet

Det binære rykksekkproblemet handler om at vi skal velge et sett med ting av forskjellig verdi og vekt slik at vi utnytter kapasiteten vår $W$ så godt som mulig.

---

07. Grådighet og stabil matching

📚Grådighet

Grådighet er en strategi for å løse problemer ved å ta grådige valg tidlig, og senere bevise at valget man tok var det optimale. Hittil har vi brukt forskjellige egenskaper ved problemet til å bestemme hvilken strategi vi vil bruke for å løse det.

• Har problemet klare steg som hverken overlapper eller splitter seg? Inkrementelt design.
• Har problemet uavhengige delproblemer? Splitt og hersk.
• Har problemet overlappende problemer? Dynamisk programmering.

I tilfeller hvor dynamisk programmering må foreta valg, kan en grådig løsning ta et valg så lenge man kan bevise at det var det rette valget.

Det er ikke mulig å bruke grådighet i alle løsninger. Problemet (og delproblemene) må oppfylle grådighetsegenskapen:

• Den globale optimale løsningen kan nås ved å ta et optimalt lokalt valg.
• Ved å ta et optimalt lokalt valg, må vi ikke ha eliminert alle mulige optimale løsninger

Dessuten vil det ikke gi mening å bruke grådighet på et problem uten optimal delstruktur.

💻Kontinuerlige ryggsekkproblemet

Det kontinuerlige ryggsegg bygger videre på det binære ryggsekkproblemet. Forskjeller er at du nå har mulighet til å velge antallet av verdien istdenfor å enten ta eller forkaste verdien.

Løsningen til det kontinuerlige ryggsekkproblemet er å ta så mye av det med høyest verdi som mulig, fordi et annet valg vil aldri klare å ta igjen det grådigste.

💻Aktivitetsutvalg

Aktivitetsutvalgproblemet handler om å velge de beste tidene på en timeplan av et utvalg med aktiviteter slik at timeplanen er så full som mulig. Dette kan for eksempel være planlegging av en forelesningsal med forskjellige forelesninger og andre aktiviteter som har lyst til å bruke salen. Da gjelder det å velge de beste aktivitetene slik at salen er brukt så mye som mulig.

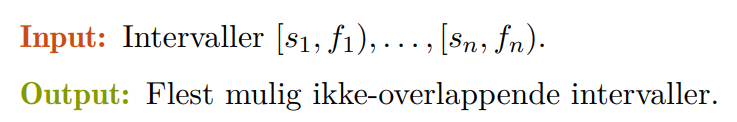
Løsningen vil være å velge aktiviteten som slutter tidligst.

💻Huffman

Huffman er en komprimeringsalgoritme som lager en enkoding basert på frekvensen til bokstavene eller tegnene i teksten. Målet med Huffman enkodingen er å lage en enkoding med kortest kodelengde. Dette gjøres ved å bygge et Huffman-tre og deretter traversere treet for å generere enkodingen basert på inputen.

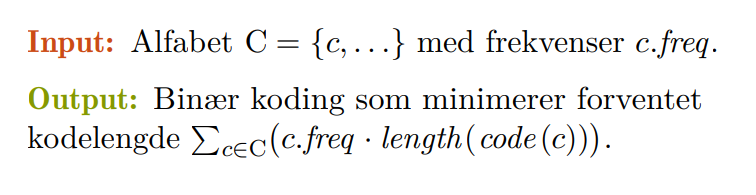
Det optimalet treet gir bokstaver som blir brukt minst de lengste kodene.

💻Gale-Shapley

Gale-Shapley er en stabil matchingalgoritme som matcher kvinner og menn (eller andre entiteter som studenter og skoler). En matchingalgoritme er stabil om det ikke finnes noen blokkerende par. Et blokkerende par er et par som foretrekker hverandre ovenfor parteren de har blitt tildelt.

Gale-Shapley er designet slik at matchingen er optimal for kvinnene, og pessimal for mennene.

---

08. Traversering av grafer

📚Grafrepresentasjoner

Det finnes flere måter å representere en graf i minne. I pensum er nabomatriser og nabolister i fokus. Representasjonene har noen forskjeller, og man sier ofte at nabomatriser er raskere, men de tar mer plass i minne.

Nabomatriser har en fordel siden det er mulig å slå opp kanter i grafen direkte, men i hovedsak bruker vi nabolister. Dessuten er det andre faktorer som veier inn på hvilken representasjon vi bruker, og som nevnt finnes det mange andre representasjoner.

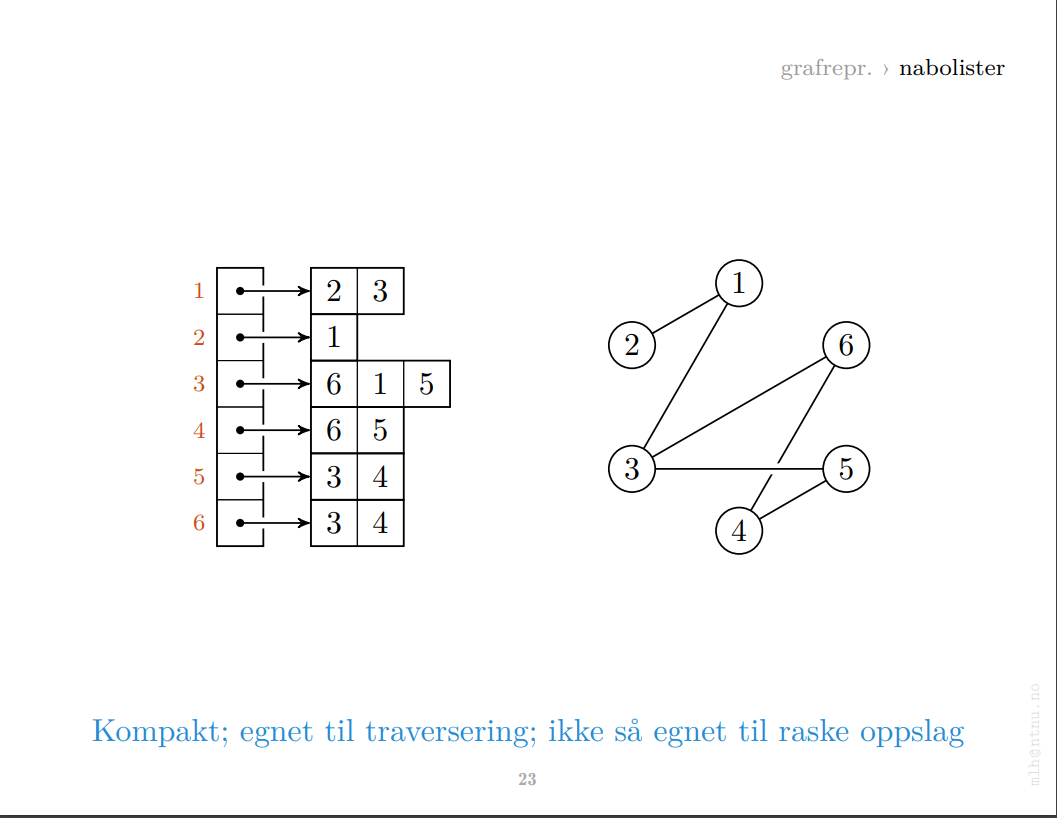
Nabomatriser egner seg til direkte oppslag. Nabolister egner seg til traversering. Nabolister tar også mindre plass dersom grafen har få kanter – men ikke ellers!

📚Traversering av grafer

Traversering av en graf kan kjøres på mange forskjellige måter, og pensum har tidligere vært innom traversering av et trær. Målet med å traversere en graf er å unngå å besøke samme node to ganger, selv om grafen har sykler. Pensum nevner to enkle måter å traversere grafer på;

• Slett noden fra grafen
• Marker noder i grafen med farger, nåværende node som grå, besøkte som svart, og ubesøkte som hvite.

💻Depth-first search

Depth-first search er en traverseringsalgoritme som går så dypt igjennom kantene i grafen som mulig før den backtracker og fortsetter i bredden. Dette skjer fordi depth-first search besøker alle nodene i grafen, og for hver node besøker alle nodene som er koblet til den nåværende noden. På denne måtten vil den alltid nå “bunnen” før den fortsetter i bredden.

• Kompleksitet på $O(V + E)$ siden algoritmen besøker hver node og hver kant.

I depth-first search er det vanlig å klassifisere nodene. Vi har følgende klasser:

• Tre-kanter: kanter som er i dybde-først skogen, altså når du møter en hvit node.
• Bakoverkanter: kanter til en forhjenger i skogen, altså når du møter en grå node.
• Forkanter: kanter som ikke er en del av DFS-skogen.
• Krysskanter: kanter som er ikke har noen anscestor/descendant relasjon

Dessuten er det interessant å merke seg at i dynamisk programmering utfører vi implisitt DFS på delproblemene.

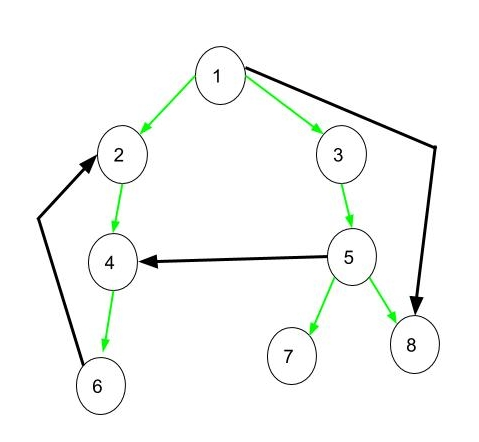
💻Breadth-first search

Breadth-first search er en traverseringsalgoritme som går så bredt igjennom kantene i grafen som mulig før den forsetter i dybden. Den kan også brukes til å finne korteste vei fra en node til alle. Breadth-first search bruker en kø over noder den ønsker å besøke, og kan på denne måten sikre seg at den søker i bredden først.

• Kompleksitet på $O(V + E)$ siden algoritmen besøker hver node og hver kant.

💻Topological sort

Topological sort er en traverseingsmetode på en DAG som gir nodene en viss rekkefølge; foreldre kommer før barn.

Det finnes flere måter å implementere topological sort på, og forelesning tar en kjapp titt på en versjon som fjerner “sources” fra grafen. En DAG har minst en “source”, en node uten noen inn-kanter.

Typisk implementasjon av topological sort bruker en algoritme lik DFS med en Stack. Her kjører man DFS over grafen, deretter sortere rangere etter synkende finish-tid.

• Kompleksitet på $O(V + E)$ siden algoritmen besøker hver node og hver kant.

---

09. Minimale spenntrær

📚Disjunkte mengder

Disjunkte mengder kommer til nytte når vi ønsker å finne spanntrær i en graf. Her kommer litt nyttig terminologi.

• Delgraf: graf som består av en delmengde av nodene og kantene til den opprinnelige grafen.
• Spenngraf: en dekkende delgraf, graf med samme nodesett som originalgrafen. (uvanlig begrep på norsk)
• Spennskog: en asyklisk spenngraf. (uvanlig begrep på norsk)
• Spenntrær: en sammenhengende spennskog, altså $|E| = |V| - 1$.

Disjunkte mengder er en effektiv måte å gruppere noder inn i sammenkoblede komponenter ved å introdusere en “parent” til hver node. Noden på topp peker deretter på seg selv.

I tillegg har hver node en rang som beskriver hvor høyt opp i hierarkiet den ligger. I andre tilfeller kan denne komme til nytte, men i tilfellet med minimale spanntrær ønsker vi kun å gruppere nodene inn i komponenter. Denne rangen brukes for å merge to komponenter (for å bestemme hvilken node som dominerer). Relevant funksjonalitet fra pensom er:

• $MakeSet$ - Lag et sett med ett element av en node. Setter parent til seg selv, og rang til 0. (I konstant tid $O(1)$)
• $FindSet$ - Finn representanten (øverste parent) til mengden som inneholder den en gitt node, ved amortisert analyse i $O(\alpha(n))$ tid.
• $Union$ - Merge to sett sammen, hvor settet med høyest rang på øverste parent dominerer den andre. Hvis begge er like, velges en vilkårlig.
• $Link$ - Lenker et sett til et annet, hvor settet med høyest rang på øverste parent dominerer den andre. (Kalt av $Union$)

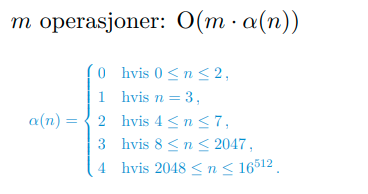
• $ConnectedComponents$ - Danne sammenkoblede komponenter av en graf. Dette kan gjøres i tilnærmet $O(V + E)$ tid (variasjon, basert på amortisert kjøretid av $FindSet$).
• $SameComponents$ - Finn ut om to noder er i samme komponent, i tilnærmet $O(1)$ tid (variasjon, basert på amortisert kjøretid av $FindSet$).

💻Generisk MST

Kanter kan ha vekter som betyr at vi til tider ønsker minimale eller maksimale spenntrær. Realistisk eksempel kan være bygging av veier mellom byer. Et minimalt spenntre er spenntreet som knytter sammen nodene med minst vekt mulig, og er et praktfult eksempel på en grådig algoritme.

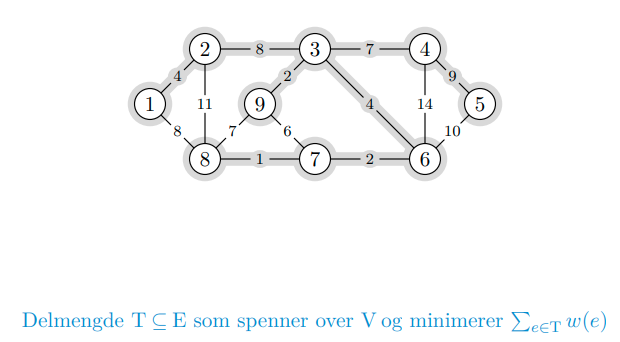
Eksempelet i forelesning bruker kantkontraksjon. Her vil hvert alternativ gi en ny, mindre delinstans. Dette passer godt til dynamisk programmering, men det er mye enklere å løse problemet på grådig vis.

Pensum bygger videre på dette prinsippet gjennom to algoritmer som opererer på litt forskjellig vis:

• Kruskal: en kant med minimal vekt blant de gjenværende er trygg så lenge den ikke danner sykler
• Prim: bygger ett tre gradvis; en lett kant over snittet rundt treet er alltid trygg

💻Kruskals algoritme

Kruskals algoritme fungerer ved å splitte opp grafen i to skoger som man jobber med; et tre man bygger til et MST, og den andre som er en skog av disjunkt mengder.

💻Prims algoritme

Prims algoritme kan implementeres på forskjellige måter, men pensum dekker en metode lik BFS ved hjelp av en min-prioritets-kø. Prioriteten er vekten på den letteste kanten mellom noden og treet.

10. Korteste vei fra én til alle

Når vi ønsker å finne korteste vei fra én til alle, ønsker vi å finne de korteste stiene fra en gitt node til alle andre noder. I tillegg vet vi at:

• En enkel sti er en sti uten sykler

• En kortest sti er alltid enkel

• Hvis det finnes en negativ sykel i veien, finnes det ingen kortest sti

  • Det finnes fortsatt en kortest enklest sti (utenfor syklen)
  • Å finne denne er et uløsp NP-hardt problem.

  

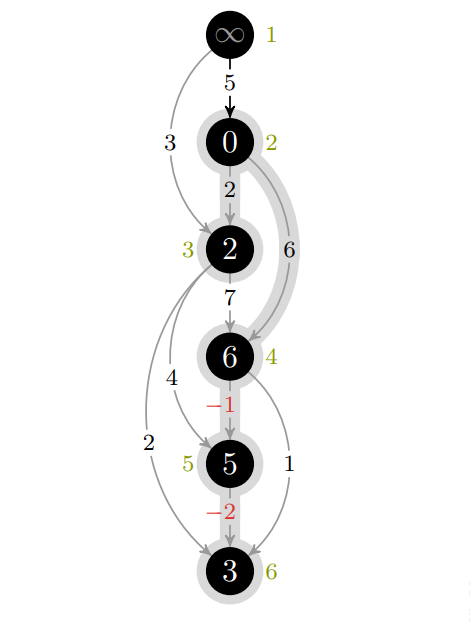
💻Dag-Shortest-Paths

Dette er en simpel algoritme for å finne de korteste stiene til alle nodene fra en gitt node gitt at det ikke finnes noen sykler (positive eller negative) i nodene som kan nås fra startnoden. Dette er fordi algoritmen bruker en topologisk sortering når den traverserer nodene i grafen.

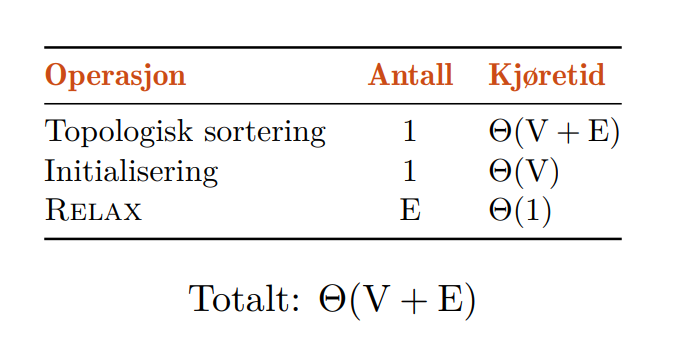
💻Bellman-Ford

Hvis vi har sykler grafen som kan nås fra startnoden kan dette løses på flere måter. Vi kan holde styr på hvilke noder som endres ved iterasjon, eller oppdatere alle kantene til ingenting endrer seg.

Teoretisk sett, skal ingenting endre seg etter $|V - 1|$ iterasjoner, siden hver node i grafen skal ha blitt besøkt så langt. Hvis ting endrer seg etter så mange iterasjoner må det finnes en negativ sykel.

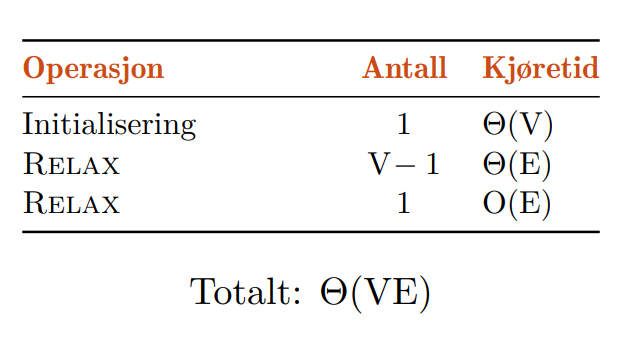
💻Dijkstras algoritme

Dijkstras algoritme tar utgangspunkt i at noden med lavest estimat må være ferdigkalkulert. Den eneste måten vekten til stien kan bli bedre er om vi hadde negative kanter. Dijkstras algoritme fungerer dermed ikke hvis grafen har negative kanter.

Kjøretiden kan videre optimaliseres ved å bruke fibonacci-heaps.

11. Korteste vei fra alle til alle

Trekantulikheten kan komme til nytte for å forstå hvordan den korteste veien kan finnes. Hvis det finnes en snarvei fra $i \to j$ som går gjennom $k$, så har vi ikke enna funnet den korteste veien fra $i \to j$.

$$\overline{AC} \leq \overline{AB} + \overline{BC}$$

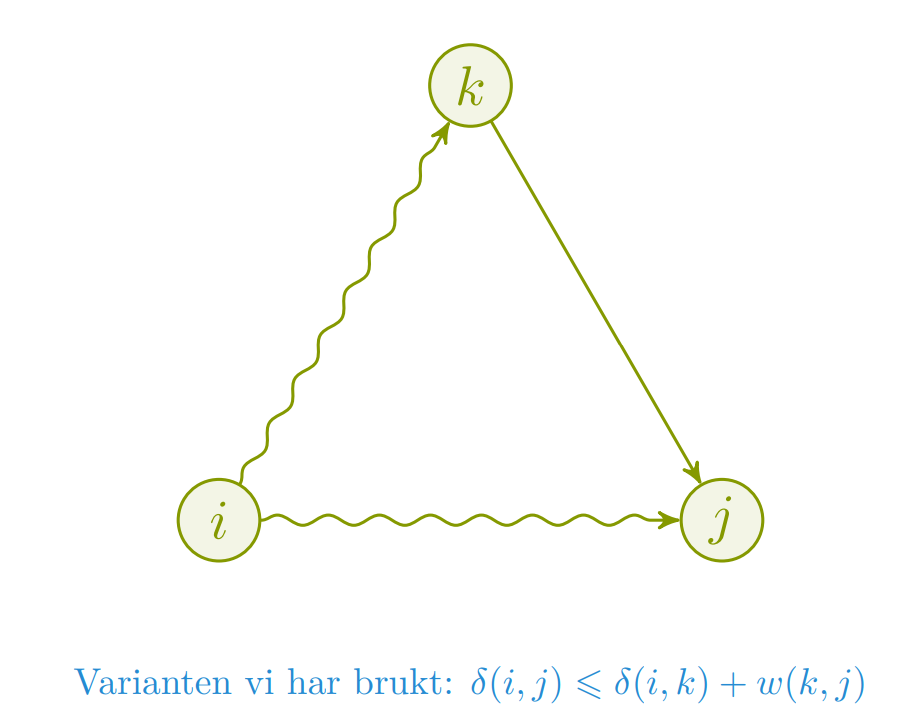
$Relax$ prosedyren vår sjekker om denne snarveien er kortere, og reparerer/gjeninnfører trekantulikheten. Når vi er ferdige, kan ikke $i \to k \to j$ fortsatt være en snarvei. ???

1. $\omega(k, j) + \delta(i, k) - \delta(i, j) \geq 0$
2. Hvis $i \to k$ og $k \to j$ finnes, finnes $i \to j$
3. $\delta(i, k) + \delta(k, j) \geq \delta(i, j)$

$Relax(u, v, \omega)$

💻Johnsons algoritme

Johnsons algoritme er en simpel måte å finne korteste vei fra alle til alle i en graf. Den bruker i all hovedsak Dijkstras algoritme for å finne korteste vei fra én til alle over alle nodene i grafen.

Det er også vanlig å returnere en forgjengermatrise $\Pi = (\pi_{ij})$

Ettersom Dijkstras algoritme ikke fungerer med negative kanter, må vi balansere alle kantene i grafen helt til det ikke finnes negative kanter. Etter utregningen vår, kan vi omjustere igjen for å finne de originale vektene.

Beskrivelse bruker Turing-reduksjoner, forelesning 13-14 begrenser dette til Karp-reduksjoner.

Når vi skal øke kantvektene, kan det virke intuitivt å øke alle kantene med like mye, men stier med mange kanter taper på denne økningen. Vi vil heller gi hver node en tilordnet verdi $h(node)$. Vekten $\omega(v, u)$ økes med differansen $h(u) - h(v)$. På denne måte vil positive og negative ledd bortsett fra det første og det siste oppheve hverandre.

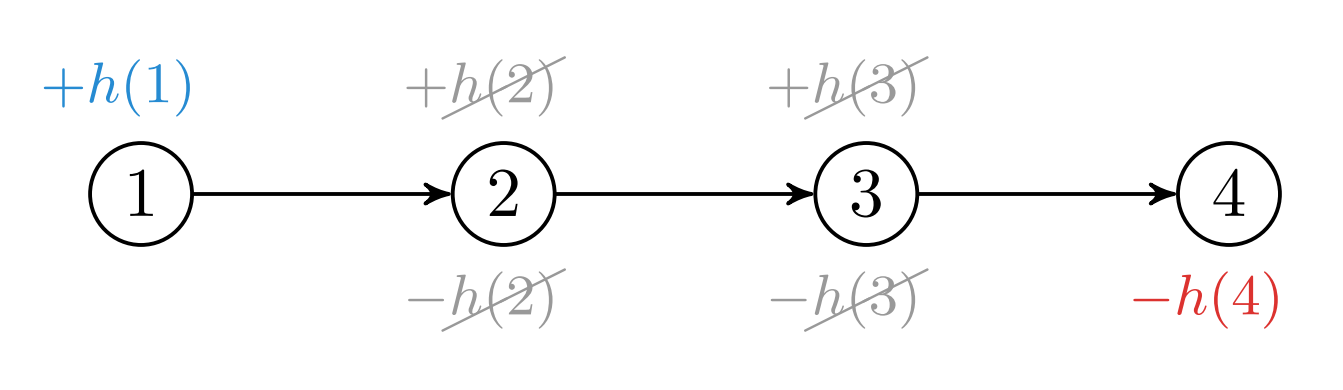
For å sikre oss at vi ikke ender opp med noen negative vekter, kan vi igjen huske på trekantulikheten som forteller oss at $\omega(k, j) + \delta(i, k) - \delta(i, j) \geq 0$. Vi kan rett og sslett legge til en ny node.

Algoritmen kjører ved å velge en tilfeldig startnode $s$ fra grafen, og deretter kjøre $BellmannFord$ for å finne ut om grafen har noen negative sykler. Deretter definerer vi differansefunksjonen $h(v)$ for enhver node basert på distansene i resultatet fra $BellmanFord$. Vi lager deretter $\hat{w}(u, v)$ med den nye vektingen til hver kant, justert med differansen $h(u) - h(v)$. Deretter kjører vi $Dijkstra$ på hver node i grafen.

💻”Matriseprodukt”

Denne algoritmen har egentlig ingen relasjon til matriseprodukt å gjøre, bortsett fra at den ene prosedyren ligner litt.

I denne algoritmen innfører vi et parameter $r$ som er antall kanter vi har lov til å besøke på stien fra $i \to j$. Vi antar induktivt at løst det for alle avstander $r - 1$, og kan dermed finne $l^{(r)}_{ij} = min_k l^{(r - 1)}_{ij} + \omega(k, j)$.

Induktivt vil vi dermed finne den korteste stien ved dette “punktet” i grafen.

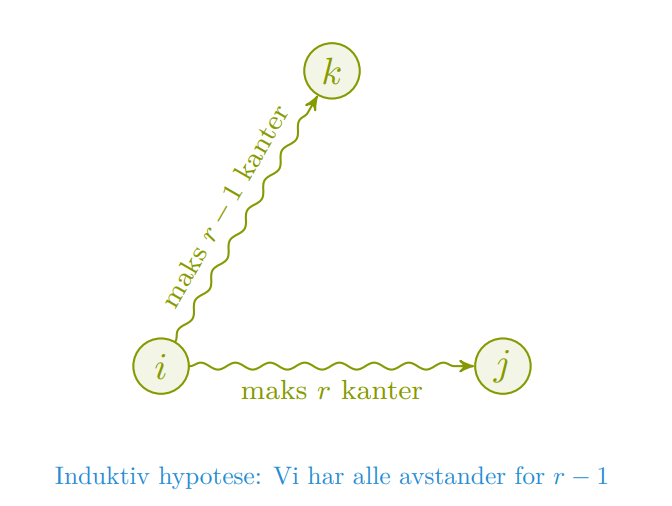
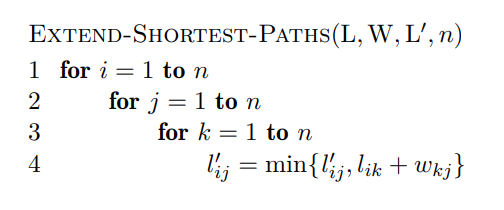
Desverre er kjøretiden på denne algoritmen $O(n^4)$. (Kanskje derfor den heter “Slow”). Bedre versjon bruker repeated squaring.

Dette resulterer i en bedre kjøretid på $\Theta(n^3 \lg n)$

📚Transitiv lukning

Gitt en graf, så ønsker vi å finne ut om enhver node $i$ kan nås fra alle de andre nodene. Her kan vi igjen løse induktivt ved å bruke trekantulikheten.

Finnes det en sti $i \to j$ som får gå innom nodene ${1, …, n}$, dvs. alle?

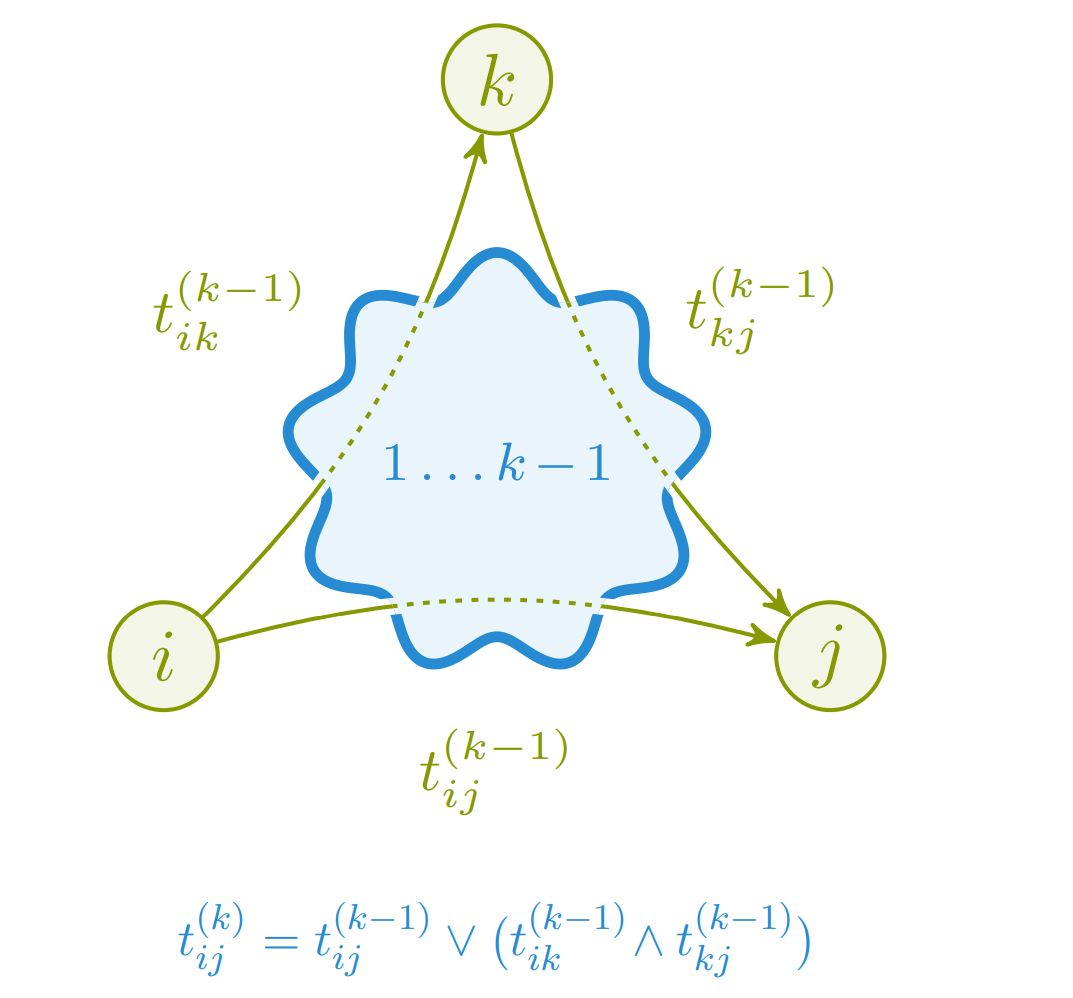
For enhver vei fra $i \to j$, kan vi enten velge den direkte strekningen $i \to j$, eller så kan vi velge $i \to j \to k$.

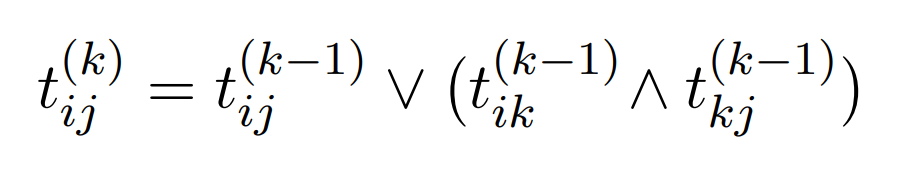
Forenklet implementasjon av algoritmen til høyre kan implementeres med en enkel tabell. Man risikerer å gå innom samme node flere ganger, men det betyr bare at vi løste et senere delproblem tidligere.

Dessuten om det finnes stier med sykler, så finnes det også en uten.

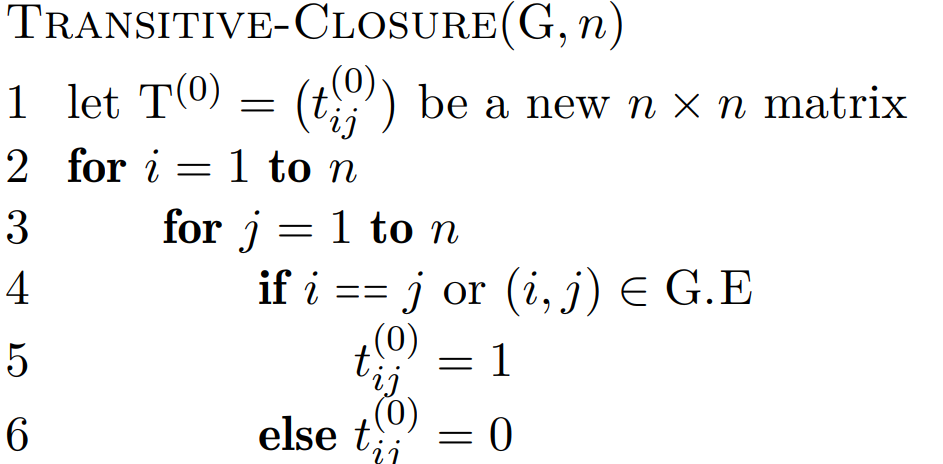
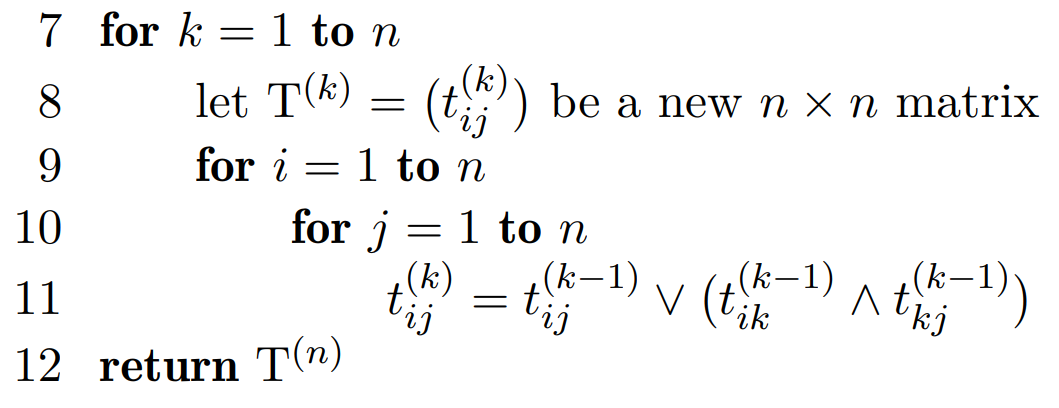
Totalt blir kjøretiden på $TransitiveClosure$ $\Theta(n^3)$. Analyse fra forelesning:

💻Floyd-Warshall

Vi har allerede sett på måter vi kan løse alle til alle problemet med Dijkstras algoritme over hver node, men vi vil gjøre det mulig å kjøre algoritmen flere typer grafer.

Ved å bygge videre på prinsippet fra transitiv lukning kan vi bruke samme måte på å velge den korteste av de to veiene som forgjenger til en hver node. Det er akkurat dette $FloydWarshall$ gjør.

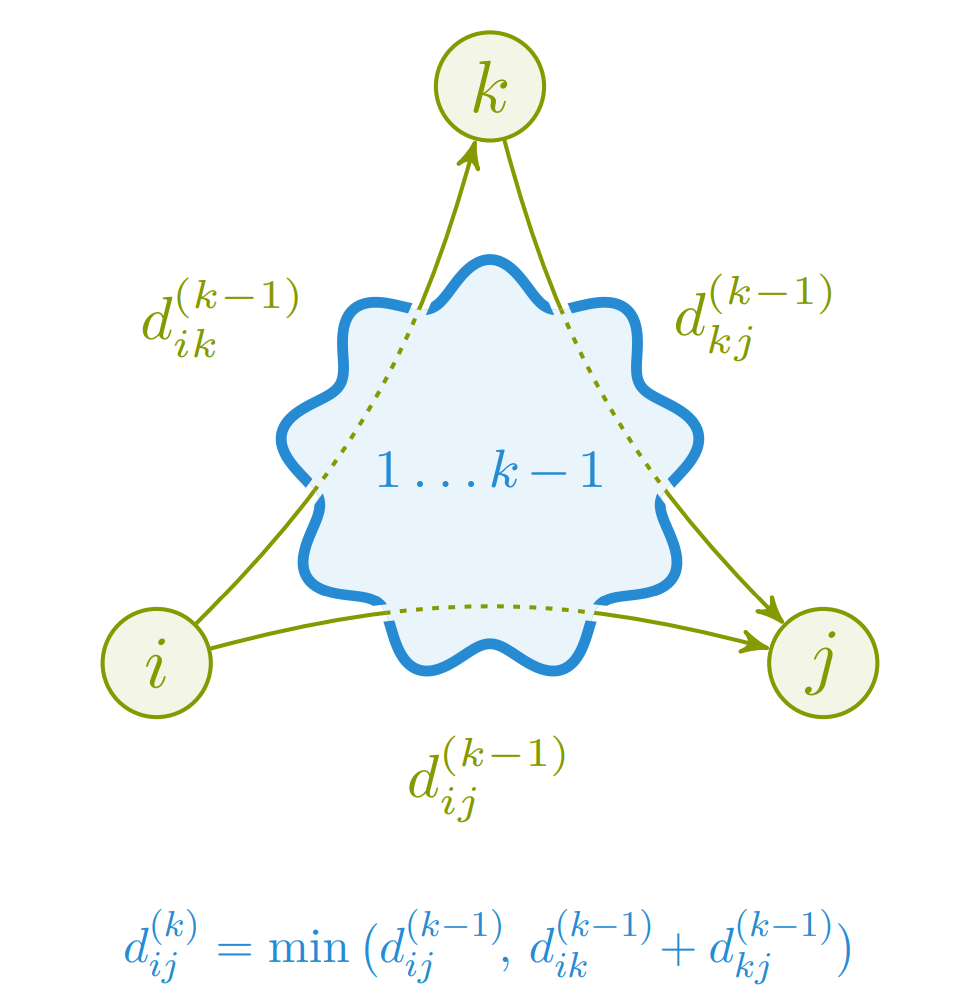
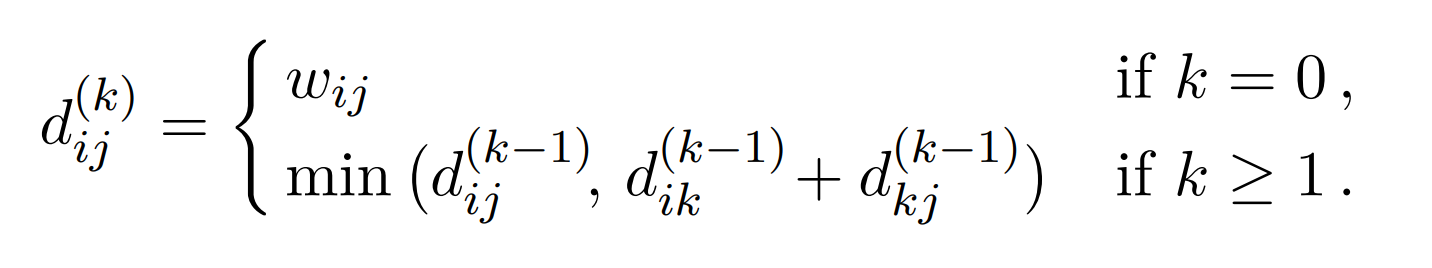
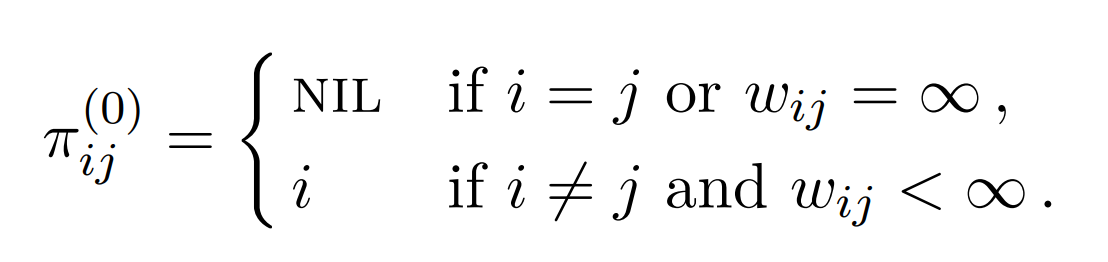
Dette resulterer i en total kjøretid på $\Theta(n^3)$. I tillegg kan det være nyttig å kunne printene veiene fra en node til en annen. Dette kan enkelt gjøres ved å besøke forgjengermatrisen.

12. Maksimal flyt

📚Problemet

Maksimal flyt er et problem på en rettet graf $G = (V, E)$. Et flytnett er grafen hvor flyten kan flyte igjennom, og den har følgende kriterier:

• Hver kant har en kapasitet $c(u, v) \geq 0$
• Det finnes ihvertfall en kilde, og en sluk $s, t \in V$
• For en hver $v \in V \implies s \to v \to t$
• Grafen har ingen self-loops
• $(u, v) \in E \implies (v, u) \not\in E$
• $(u, v) \not\in E \implies c(u, v) = 0$

Den resulterende flyten er en funksjon $f : V \times V \to \R$. Flyten på en kant kan aldri være større en kapasiteten på kanten, altså:

• $0 \leq f(u, v) \leq c(u, v)$
• For en kant $u \neq s, t$, gjelder $\sum_v f(u, v) = \sum_v(v, u)$

Flytverdien $|f| = \sum_v f(s, v) - \sum_v f(v, s)$ er flyten som kan nås fra source til en gitt node.

Hvis du har flere kilder og sluker, legger man til en super-kilde og en super-sluk

Det minimale snittet er gitt etter å ha kjørt maksimal flyt på en graf. Den skaper en partisjon i flytnettet etter at sluket til grafen ikke kan nås lengre. Snittet i flytnettet er en partisjon $(S, T)$ av $V$. $s \in S$ og $t \in T$.

Netto-flyten beskriver flyten som mellom partisjonen.

$$f(S, T) = \sum_{u \in S}\sum_{v \in S}f(u, v) - \sum_{u \in T}\sum_{v \in T}f(u, v)$$

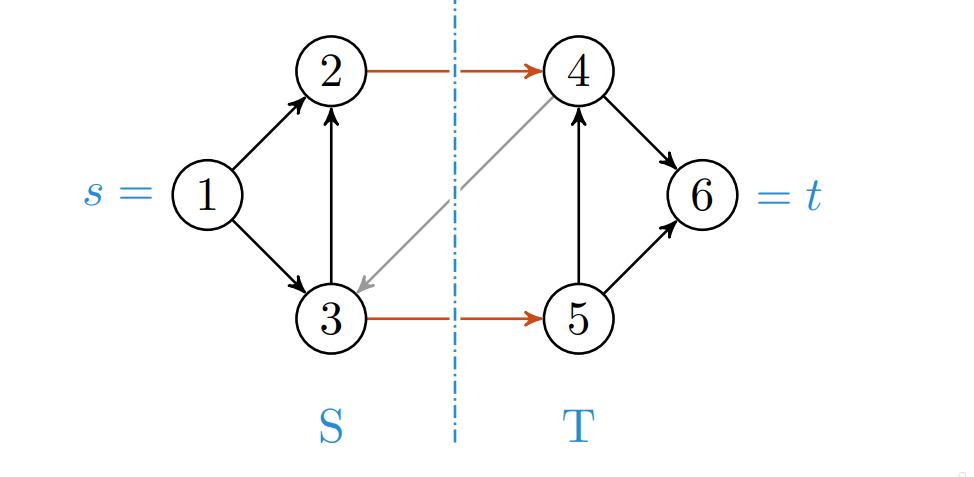
Kapasiteten blir $c(S, T) = \sum_{u \in S}\sum_{v \in T} c(u, v)$.

Til slutt beskriver Lemma 24.4: $f(S, T) = |f|$. Bevis for dette krever en del utregning, men er ganske rett frem. Videre Corollary 24.5: $|f| \leq c(S, T)$.

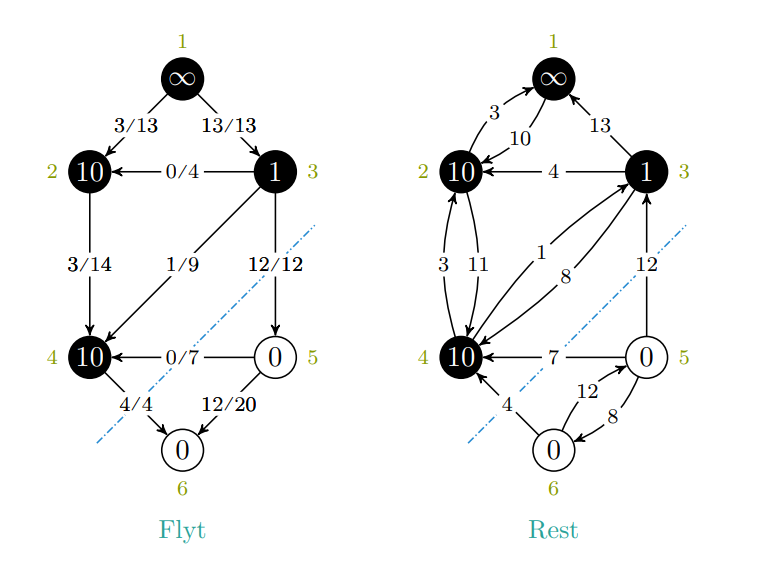
Maksimal flyt fører dermed til det minste snittet. Videre forteller helltallsteoremet (24.10) at for heltallskapsiteter $c(u, v) \in \N$ gir $FordFulkerson$ og andre flytalgoritmer basert på $FordFulkerson$ en heltallsflyt $|f| \in \N$.

📚Reduksjon til flyt

Flyt kan nesten regnes som en designmetode siden vi kan redusere mange problemer til flytproblemet. Pensum ser på et par måter å bryte ned større problemer til flytproblemer. Blant annet:

• Biparitt matching, gjør om hver donor og mottaker til sink/source hvor kantene har en kapasitet på 1, deretter lag en supersource/supersink som vanlig. Greit å notere seg at $EdmondsKarp$ er ikke den mest effektive måte å gjøre dette på. I rekonstruksjonen representerer kanter med flyt matchingen.

  

• Legekontor hvor man ønsker minst én lege på vakt hver dag i feriene, men hver lege skal jobbe maks $c$ feriedager totalt, og maks en gang per ferie. Denne løses ved å gjøre legene om til sources med kapasitet $c$, og lag en source med kapasitet 1 for hver feriedag.

• Bildesegmentering for å separere forgrunn og bakgrunn kan løses ved å gjøre hver piksel til en node, og kapasiteten fra kilde tilsvarende “forgrunnsaktighet” og kapasitet til sluk “bakgrunnsaktighet”. Kapaisteten mellom noder tilsvarer hvor like de er. Her vil det minimale snittet skille forgrunn fra bakgrunn.

• Veisperring kan løses ved å gjøre åstedet til source, og hvert sted man kan sette opp sperringer til sinks med kapasitet basert på hvor fort forbryterne kan bevege seg.

💻Biparitt matching

Designmetoden som brukes for biparitt matching baserer seg på å gjentatte ganger konstruere et nytt, enklere problem, som gir en forbedring av den opprinnelige instansen.

Vi øker matchingen ved å finne stier fra venstre til høyre (i en liggende graf). Kanter som brukes i matchingen blir snudd baklengs slik at det er mulig å endre på de hvis det viser seg at det er mer optimalt senere.

Hvis vi for eksempel finner ut at en donor kan kun matches med første resipient (men vi har allerede gitt første resipent en donor), kan vi bruke dette til å oppheve matchingen.

📚Ideer

Det samme gjelder for flyt. Vi har kanskje fått frem én enhet, men hvis vi har en forøkende sti (sti som gir bedre resultat en nåværende), har vi lyst til å sende tilbake enheten. Den originale enheten (eller flyten) sendes tilbake hvor den kom fra, og så finner vi en ny vei frem. Da får vi igjen en forøkende sti, og flyter fremover, og opphever den bakover til flyten når der den kom fra.

Et restnett (residual network) er et nettverk likt flytnettet, bortsett fra at kantene mellom nodene er fremoverkanter ved ledig kapasitet, og bakoverkanter ved flyt.

En forøkende sti (augmenting path) er en sti fra kilde til sluk i restnettet. Langs fremoverkanter kan flyten økes, og langs bakoverkanter kan flyten omdirigeres. Det er altså en sti hvor den totale flyten kan økes.

Det er dermed nyttig å finne ut hva potensialet (eller restkapasiteten) mellom to noder er. Hvor mye kan vi øke flyten fra $u$ til $v$?

💻Ford-Fulkerson

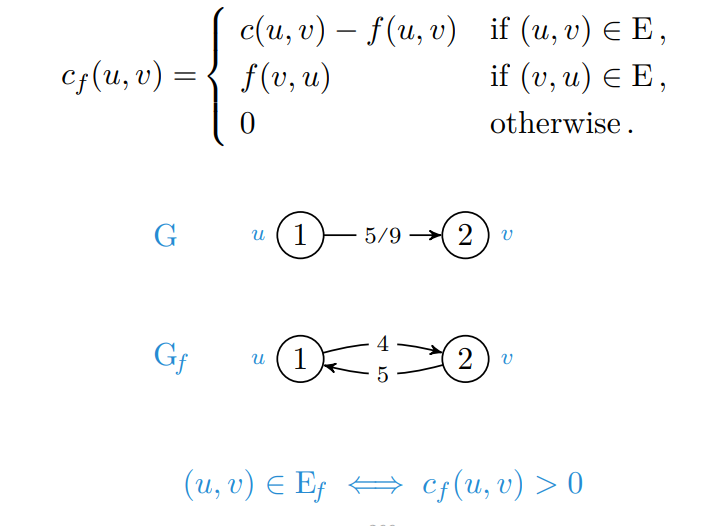
$FordFulkerson$ er en generell metode for å finne den maksimale flyten gjennom et nettverk. En versjon av $FordFulkerson$ er $EdmondKarp$ som bruker en BFS. Ford-Fulkersom fungerer ved å:

1. Finn forøkende stier så lenge det går
2. Deretter er flyten så stor den kan bli.

Dette gjøres som regel ved å finne den forøkende stien, deretter finner man flaskehalsen i stien, og oppdaterer flyt langs stien med denne verdien.

En mer konkret beskrivelse av algoritmen finnes i pensum:

Alternativt kan man flette inn BFS ved å finne flaskehalser underveis. Hold deretter styr på hvor mye flyt vi får frem til hver node, og traverser kun noder vi ikke har nådd frem til enda.

Denne implementasjonen står ikke i boka, og det er ikke krav å kunne denne i detalj.

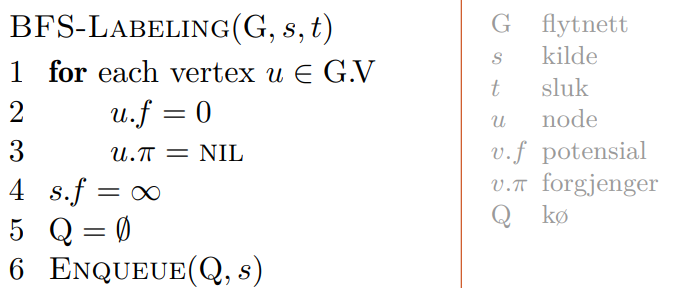
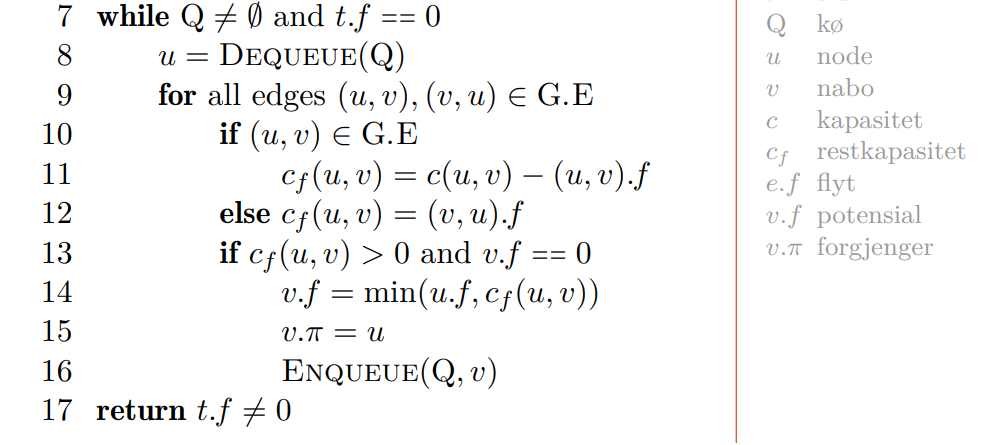
Når vi hr kjørt Ford-Fulkerson kan vi finne det minimale snittet direkte fra resultatet. Forelesningsnotatet inneholder mer om bevis på korrekthet.

Kjøretiden på Ford-Fulkerson kan gå ille hvis vi ikke bruker BFS. En graf som ser slik ut, vil kunne sende flyten fra og tilbake på noden med 1 kapasitet flere millioner ganger.

Med irrasjonale kapasiteter kan vi ikke garantere at Ford-Fulkerson terminerer,

Hvis vi bruker BFS, vil får vi en kjøretid på $O(VE^2)$ for å finne forøkende stier.

Pensum har en lengre forklaring på hvorfor vi får $O(VE)$ i indre løkke.

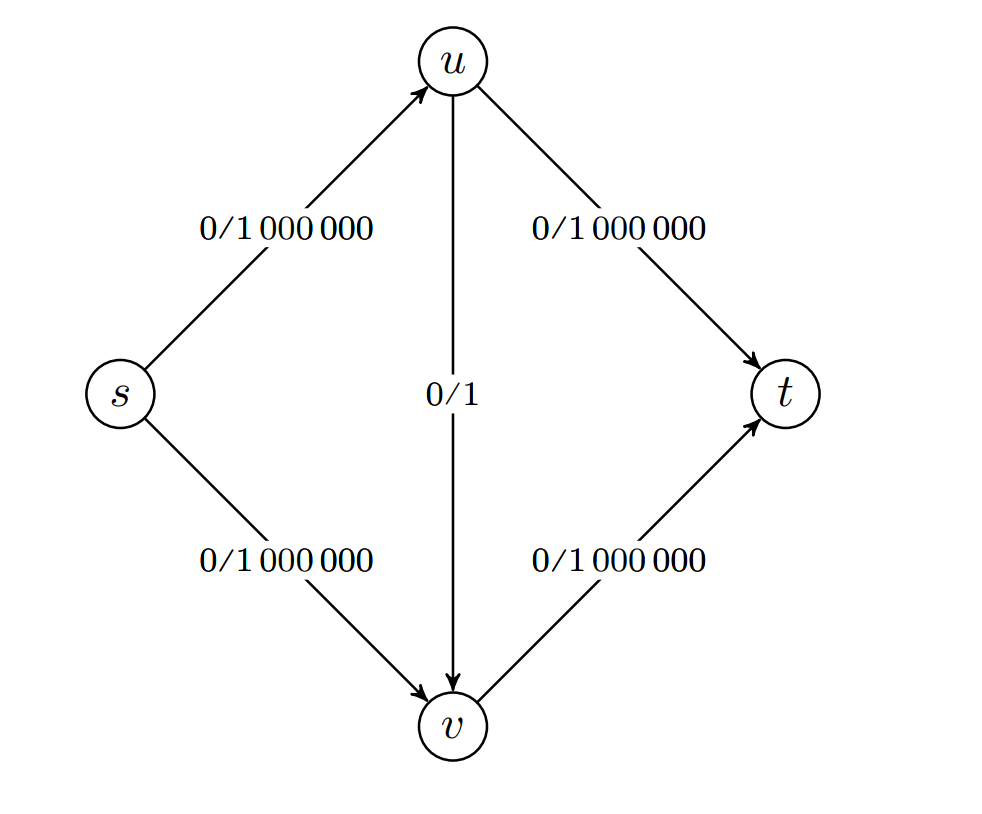
https://folk.idi.ntnu.no/mlh/algkon/flow.pdf

13. NP-kompletthet

📚Reduksjon

I denne forelesningen betegner reduksjoner Karp-reduksjoner, eller “many-one” reduksjoner som tar polynomisk lang tid.

Vi ønsker å beskrive problemer sin vanskelighetsgrad. Det er teoretisk mulig å finne absolutt vanskeliggrad av et problem, men det er lite nyttig, så vi vil heller sammenligne og kategorisere problemer.

Et eksempel på en Karp-reduksjon fra forelesning:

Gitt en kiste $A$, og en kiste $B$ hvor nøkkelen til $A$ ligger inni $B$. Ved reduksjon er det dermed åpenbart at det ikke kan være vanskeligere å åpne $A$ enn det er å åpne $B$.

Hva “minst like vanskelig” betyr kommer an på reduksjonene, men i vårt tilfelle bruker vi polynomiske reduksjoner som betyr at problemene kan løses i polynomisk tid.

Hvis vi ønsker å løse problemet “har en graf en kort sti mellom node $u$ og $v$” kan vi redusere dette ned til å finne korteste sti mellom nodene. Det er dermed åpenbart at å finne ut om det finnes en kort sti, er minst like vanskelig som å finne korteste sti.

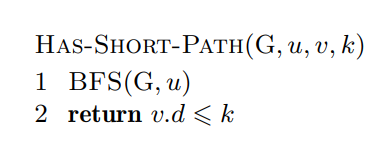
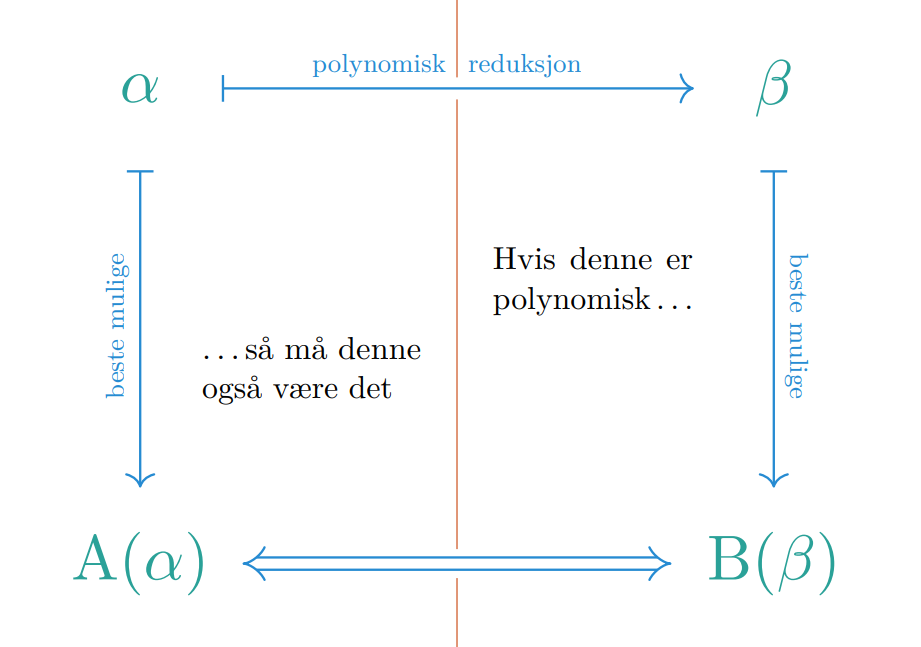
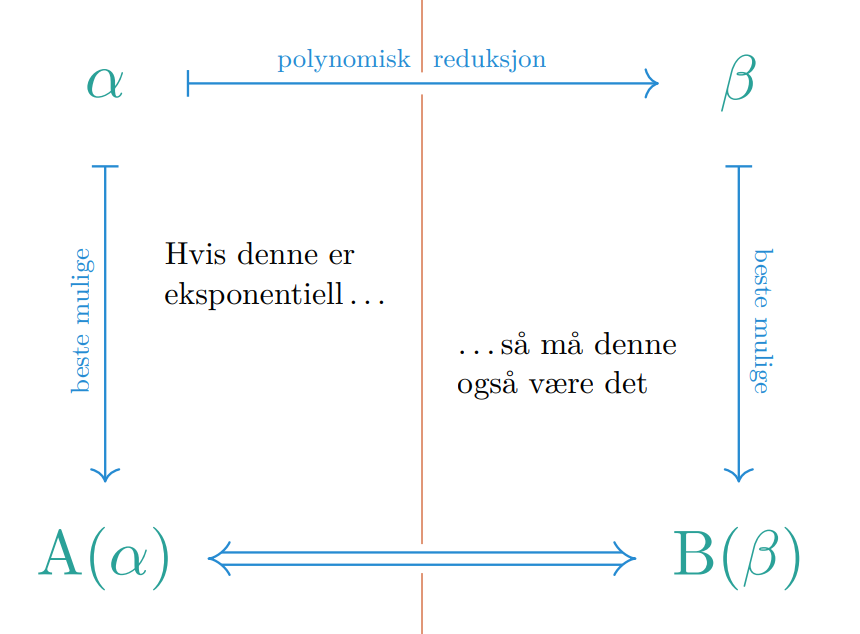
Hvis vi har et problem $\alpha$ som vi kan polynomisk redusere til et annet problem $\beta$ som også er polynomisk, er det åpenbart at vi kan bruke løsningen $B(\beta)$ for å lage en løsning $A(\alpha)$.

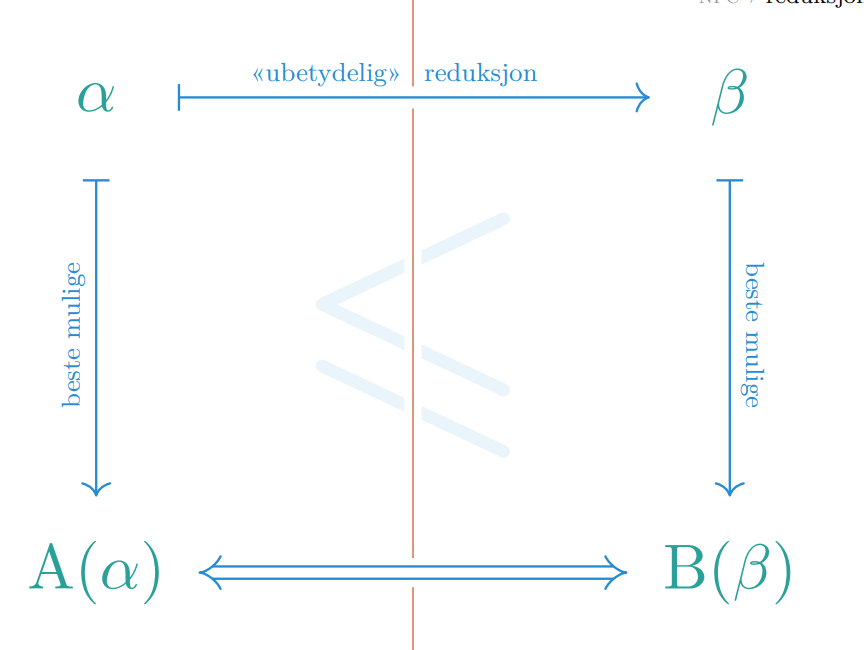
Vi kan redusere Hamilton-sykel problemet ned til Long-Path problemet i polynomisk tid, så det betyr at $HamCycle$ kan umulig være vanskeligere enn $LongPath$, og $LongPath$ er minst like vanskelig som $HamCycle$.

På denne måten kan vi også redusere perfekt matching til $HamCycle$, og det betyr at $Match$ kan umulig være vanskeligere enn $HamCycle$, og dermed ikke vanskeligere enn $LongPath$. Det eneste problemet er at vi ikke vet hvordan vi kan finne en løsning på $LongPath$.

📚Verifikasjon

Beslutningsproblemer er problemer vi kan verifiserer et sertifikat for et ja-svar. Hvis vi lurer på om $X$ finnes, kan vi bruke verifikasjonsfunksjonen til å sjekke enhver mulig $X$ for en instans. Verifikasjonsmetoden i dette tilfellet kjører i polynomisk tid slik at det er mulig å verifisere det. Hvis svaret er “nei”, så har vi ingen sertifkat for problemet, ingenting å verifisere.

Et beslutningsproblem stiller rett og slett spørsmålet “finnes det et sertifikat for at svaret er ja?” for et slikt sertifikat skal finnes hvis, og bare hvis svaret er “ja”.

• Problemklassen P er problemer som kan løses i polynomisk tid.
• Problemklassen NP har ja-svar sertifikater som kan sjekkes i polynomisk tid. Problemer i NP som også er i P er selvfølgelig løsbare i polynomisk tid.
• Problemklassen NPC kan vi ikke løse, men vi kan verifisere de i polynomisk tid. NP-komplette problemer er subsettet av NP som alle andre NP problemer kan reduseres til i polynomisk tid.
• Problemklassen NPH kan ikke løses eller verifiseres, men de som også er i NPC kan selvfølgelig sjekkes i polynomisk tid. Dette er problemer som er minst like vanskelige som NPC, men de trenger ikke å være i NP, og trenger ikke å være beslutningsproblemer.
• Problemklassen co-NP har nei-svar som kan sjekkes i polynomisk tid.

Dette betyr at hvis man finner et bevis for å løse et NP-komplett problem, kan man løse alle andre NP problemer.

Det er også praktisk å se på beslutningsproblemene som mengder av instanser (bitstrenger) der svaret er ja. En slik mengde er et formelt språk.

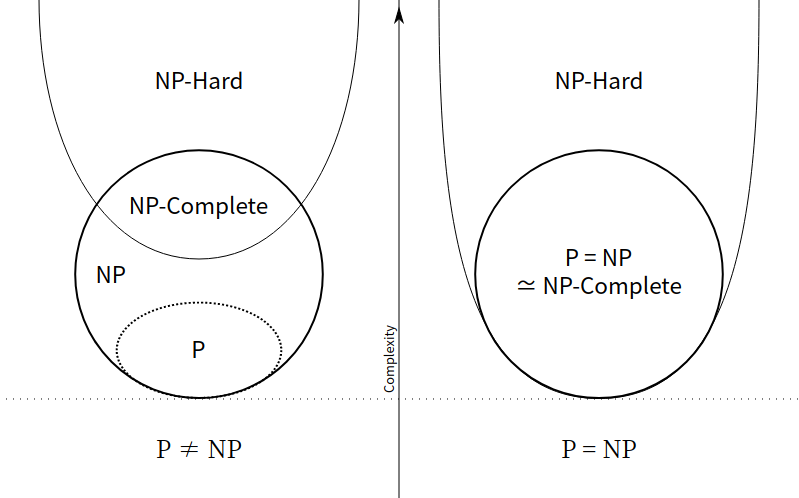
What are the differences between NP, NP-Complete and NP-Hard?

📚Kompletthet

Vi har et univers av problemer og vi kan sammenligne dem. Det gir faktisk opphav til et sett med maksimalt vanskelige problemer. Disse kalles komplette for klassen NP under polynomiske reduksjoner.

Hvis vi har en mengde med kister, og en ekstra kiste $K$ som har nøkkelen til alle de andre, så kan vi redusere åpne alle kistene til åpne $K$. Kompletthet er en universalnøkkel for alle problemene. Finner vi nøkkelen her, kan vi løse alle de andre problemene.

Slik ser vi for oss at hierarkiet til problemene er, selv om det ikke er helt mulig å vite. Det finnes også mange andre klasser med problemer, og det er mange mulige scenarier. Problemet er at ingen vet hva som stemmer.

Se slides for bedre beskrivelse

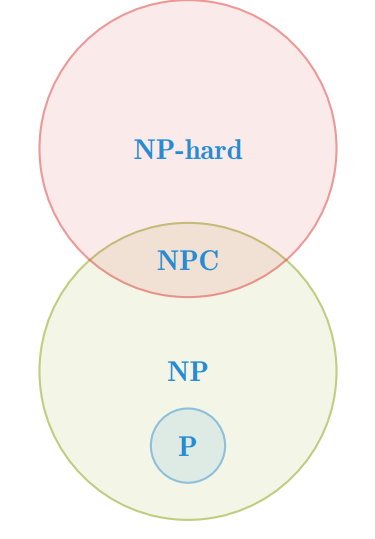
Hvis det har seg slik at $P = NP$, kan vi ikke bare svare på om det finnes et sertifikat, men vi kan rekonstruere sertifikatet. Med andre ord, kan vi løse beslutningsproblemer, så kan vi løse søkeproblemer også, og finne gyldig output.

💻Oppfyllbarhet

Oppfyllbarhetsproblemet var det første problemet som ble bevist til å være NPC. Det går ut på å finne ut om det er mulig at en logisk krets sine inputs kan bestemme om det er mulig at output er 1.